Determination of local gravimetric geoid

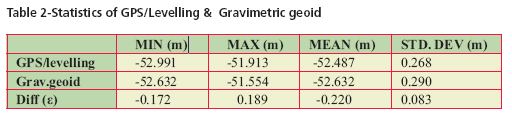
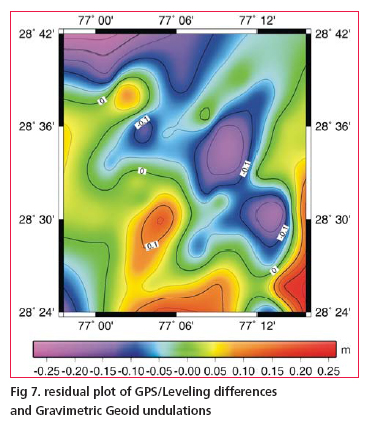
Evaluation of Geoid Model

Differences between the GPS derived ellipsoidal heights and the levelling heights of bench mark of national control network are generally being used for geoid evaluation. In present study the GPS/levelling differences were derived by making GPS observations on 50 nos. of stations and connecting them to bench marks of Indian vertical control network by running precision leveling lines. GPS data was processed using BERNESE Software Ver.4.2 and an accuracy of derived ellipsoidal height of the order of few cm has been achieved. None of these stations was included in the geoid modeling process. The quantities to compare are the geoidal heights from the gravimetric geoid Ngrav and the corresponding geoidal height NGPS from GPS/leveling observations. The misfi t ε ε = NGPS – Ngrav includes datum differences, systematic errors and subsidence /uplift in the levelling, as well as errors in the gravimetric geoid. The statistics of the GPS/levelling differences and heights from gravimetric geoidal model have been presented in Table 2 and Fig. 7 shows the contour plot of the differences. The above results clearly show a close matching between the gravimetric geoid and GPS/leveling differences and probably described the advantage of using dense gravity data. There is hardly any longitudinal variations noticed for the geoid but it has shown the traces of northward gradual slope which may be evident more clearly when computations are taken for a larger region. Though the results still contain the systematic differences between local levelling network and the gravimetric geoid but major contribution of these errors has been nullified due to the fact that test area is considerably small and terrain effect is almost negligible because of smooth topography of the region.

Conclusions

This paper has described a brief review of some of the important aspects involved in computation of gravimetric geoid model in Indian context. The use of generalized scheme along with modifi ed Stokes Kernel in remove-compute-restore technique has been successful to a great extent in computation of geoid model from dense gravity anomaly data of Delhi area. The study has fi rmly shown that EGM96 can be effectively used for gravimetric geoidal modeling in India notwithstanding its own shortcomings provided that the other aspects of the methodology are explicitly designed and followed carefully. The procedure of analytical solution of Stokes integrations with spherical cap of radius of o.5° using dense gravity data has worked well and achieved an accuracy, in absolute sense, of the order of 20 cm as determined from comparison with GPS/leveling differences making it an alternative to conventional method of leveling, suitable for most of the mapping applications. However a signifi cant size of errors in GPS determined ellipsoidal heights is always expected from the various error sources. Even with a very detailed error modeling of all the possible source effects the achievable accuracy of GPS ellipsoidal height is always considered to be less than the horizontal positional accuracy. Hence the extent of misfit between the gravimetric geoid and GPS/levelling difference should not be always viewed entirely due to error in gravity measurements or inadequate geoidal modelling procedure.

Acknowledgements

The authors gratefully acknowledge the consistent effort made by officers and staff of satellite geodesy and project survey wings of G&RB for their excellent work of field data collection, processing and typing of this manuscript.

References

Burrared, S.G.,1910, Levelling of Precision in India, GTS Vol. XIX, Survey of India, Dehradun

Forsberg ,R.(1994) Terrain effects in Geoid computation, Lecture notes, Int. school for the determination and use of geoid, Milano.

Heiskanen, W,Moritz , H (1967) Physical Geodesy, Freeman, San Fransisco.

Lemoine FG, Smith D, Smith R, Kunz L, Pavlis E, Pavlis N, Klosko S, Chinn D, Torrence M,Williomson R, Cox C, Rachlin K, Wang Y, Kenyon S, Salman R, Trimmer R, Rapp R, Nerem S (1996) The development of NASA GSFC and DMA joint Geopotential model, Proc. of International Symposium on Gravity Geoid and Marine Geodesy, University of Tokyo.

Morelli C,Gantar C,Honcaslo T,Mc connel RK,Tanner TG,Szabo B,Uotila,U,Whalen CT(1971) The International Gravity Standardisation Network(IGSN71),Bull
Geod.Sp. publ 4.

Schwarz K.P., Sideris M.G. and Forsberg R. (1990).The uses of FFT techniques in Physical Geodesy. Geophysical J. Int, pp.485-514.

Vanicek P , Sjöberg LE(1991) Reformulation of Stokes’ theory for higher than second-degree reference fi eld and modifi cation of integration kernels,J. Geophys. Res. 96(B4):6529-6540.