The Missing Observation: Orthometric Height

Mohamed Eleiche Geoinformatics Consultant GeoTiba Systems

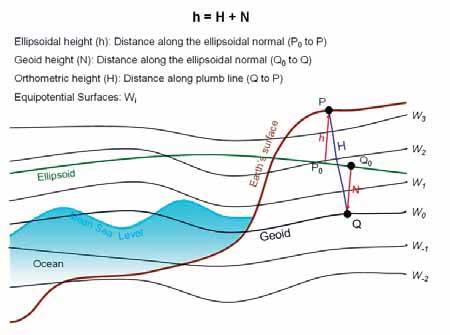
Although the revolutionary GPS observations system delivers instantaneously the coordinates of a point with high accuracy, still another quantity, which is the orthometric height, needs also to be determined. Unfortunately, neither the orthometric height nor the geoid undulation can be observed directly. The aim of this paper is to declare the limitations of GPS observations and the importance of orthometric height and how it is computed in the traditional GPS work.

Introduction

The determination of the coordinates of a point on the earth surface with high accuracy is a real contemporary challenge. Although we are today (2011) equipped with arsenal of unprecedented electronic surveying devices (GPS) receiving positional signals from dozens of satellites orbiting the earth in addition to online public and private geodetic networks broadcasting measurement enhancement, we still didn’t reach the required positional accuracy over our earth globe. The GPS delivers two quantities, which are latitude and longitude, and still the third quantity, which is the orthometric height, is not directly observed. The modern geodetic accuracy requires a centimeter level for the three coordinates describing a position on earth.
The purpose of this paper is to declare the real capabilities of GPS and the importance of the orthometric height in geodetic measurements and how it is currently computed.

Combined Coordinate Reference Systems (CRS) in Geodesy

In physics, usually a unique Coordinate Reference System (CRS) is used to describe a position in three dimensions (or four dimensions) quantities. However, the earth shape is very complex and irregular, and it is in dynamic state and always changing due to several parameters such as earth rotation around its vertical axis, earthquakes, and other. In geodesy, two different CRS are used to describe the position on earth surface and each one has different observation methodology. This combined (dual) CRS used in geodesy is a main source of confusion and requires bold clarification.

Figure 1: Relation between geoid and ellipsoid (Courtesy Natural Resources Canada www.nrcan.gc.ca)

The first CRS is the ellipsoid system, recently based on WGS84 ellipsoid with its center coincides with earth geocenter. This CRS is also known to be geometrical 3D reference system, as the position of a point can be achieved by geometrical observations.

The second CRS is the geoid, which is not a geometrical shape, rather it is a physical (geophysical) reference. The geoid is densely defined in geodesy and geosciences’ literature. The most common definition for geoid is its representation to the geopotential surface, where the gravity force is equal. The water surface of the earth is coincident with the geoid inside the water on earth (75% from earth surface is water), and it is continued under the earth crust as imaginary surface. Assuming that is the potential energy of the geoid (at the present mean sea level), by definition:

It is required to compute the value of the height (H) of the observed point above (or below) the geoid. This height (H) is called orthometric height or physical height, as shown in Figure (1).

GPS Observations

Before GPS, the latitude and longitude were computed from geodetic observations, such as baselines, triangulation, and trilateration. After the GPS era, these two quantities are computed directly from GPS observations in addition to the height of the observed point above the WGS84 ellipsoid, which is observed and determined directly for the first time in the history of geodesy. The GPS delivers four quantities for the observed point, which are the latitude (L), the longitude (B), the height above (or below) ellipsoid (h) and time of observation (t). The quantities (L, B) are angular values in degrees and ellipsoid height (h) is in meters. All these quantities are delivered in the famous CRS named WGS84.

Orthometric (Physical) Height

By its definition, the physical height (H) of a point is the distance between the point and the geoid surface as shown in Figure (1). Unfortunately, there is no direct methodology known to compute the orthometric height (H) directly. The geoid itself is an imaginary subsurface and it has only geophysical definition with a defined potential energy.

The Classical Leveling Technique

Long away, the water surface of the earth was considered as a homogenous equipotential surface and a datum for vertical observations. Hence, most of the height measurements were measured by leveling from the Mean Sea Level (MSL). Scientists and engineers criticize the leveling for main reason, it uses horizontal plan (datum) for relative height difference while the datum used for height is the geoid which is not horizontal, rather it’s irregular.

Geoid Undulation (N)

After the GPS era, a new quantity was observed directly, which is the ellipsoid height (h). The direct computation of ellipsoid height (h) motivated the observation of the undulation (N) between the geoid and the ellipsoid WGS84, and compute the orthometric height (H) from the equation relating (h, H, N) at a single point:

H = h – N

In case (N) is known and with the value of (h), the orthometric height (H) can be computed. Unlikely, the geoid undulation (N) cannot be observed directly at point (P). It needs gravity measurements and sophisticated computations. The separation (N) between the geoid surface and the WGS84 ellipsoid vary approximately to the range between -100m to +70 m all over the earth globe.

The GPS observations deliver the ellipsoid height at the point of interest, which is considered a revolution in geodesy, where before this value was difficult to compute or determine directly. Also, there are several modern methodologies for computing the geoid up to one centimeter accuracy using satellite technology, field gravimeters, and advanced mathematical models.

Practical GPS Observations

In traditional GPS observations, it is required to deliver the coordinates of the observed points in the geodetic dual CRS (L, B, H), and this impose the necessity to compute the orthometric height (H). The common practice is to model the geoid surface (N) in the observation area and compute the orthometric height from H = h – N.

Conclusion

In geodesy, two coordinate reference systems (CRS) are used, geometrical CRS and geophysical CRS. The GPS delivers all the required observations for the geometrical CRS. It is a real revolution in geodesy, it introduced a fast and accurate technique to determine the latitude and longitude of a point, in addition to the value of its ellipsoid height. However, still an important value not yet directly observed for the geophysical CRS, which is the physical (orthometric) height. Leveling is not an accurate methodology for physical height measurements. The value of the geoid undulation from ellipsoid is an important quantity and is necessary to be known. The traditional GPS observations include geoid modeling for area of interest for the computation of the orthometric height.
Finally, a new methodology is required to compute directly in field the geoid undulation and orthometric height.