| GNSS | |
Simple and effective RAIM technique for multiple outliers
In this paper, the conventional w-test is improved and the forwardbackward method is used for multiple outliers. Two observations are flagged as outliers in each iteration by the extended w-test method |
 |
|
 |
|
 |
|
With the development of modern Global Satellite Navigation System (GNSS), the accuracy performance of satellite positioning and navigation is obviously improved, which extends the range of applications greatly for the GNSS receivers. The integrity of GNSS plays a central role in extending the use of receivers. Since it is located at the end of the integrity processing chain, RAIM has the advantage of timely monitoring the receivers’ local errors compared with the other ways.
The existing Receiver Autonomous Integrity Monitoring (RAIM) techniques are generally based on a single outlier assumption model. However, with the increasing number of available satellites, the probability of multiple satellites failure increases simultaneously. Meanwhile the GNSS measurements are affected by gross errors in signaldegraded scenarios (e.g., urban canyons and mountain areas).Therefore the RAIM techniques for multiple outliers need more attention and analysis. The new algorithms should be relatively simple in order to minimize the alarm time and not affect the sampling rate of the receiver.
Currently the analysis of RAIM techniques for multiple outliers has focused on the self-consistency of Least Squares (LS) residuals, but there are still some other different approaches. The limitations of the conventional w-test procedure when identifying multiple faults are analyzed in detail in [1]. To maintain algorithmic simplicity, the extended algorithm only deals with the correlation between w-test statistics after obtaining the initial adjustment.
Reference [2] introduces and modifies three kinds of RAIM techniques for multiple blunders used in urban scenarios. They are “Observation Subset Testing”, “Forward-Backward Method” and “Danish Method”. At the same time, the paper also points out the validity of separability check in avoiding excluding the good measurements. Reference [3] takes advantage of the great redundancy of modern GNSS and the new scheme identifies two outliers in each iteration. However some good measurements are sacrificed. If the number of outliers is known in advance, the parity vector method can be used to identify multiple faults as in [4,5], but it has much matrix operation leading to a large amount of computation. By using measurements collected on different epochs or introducing some constraints, the error of each satellite lost by LS integrity algorithm can be reconstructed as in [6,7]. Reference [8] takes into account the fact that fault detection is simpler than fault exclusion.
The initial fault-free constellation is firstly obtained and the remaining satellites are added into the constellation one by one. The new method only uses the approach of fault detection to implement integrity monitoring.
In this paper, the forward-backward and extended w-test method which identifies two outliers each iteration are combined. Meanwhile the separability check is executed. In the backward process, pseudorange residuals instead of LS estimator are used to determine whether the exclusion is correct. Thereby the amount of computation is reduced.
Conventional W-Test
Due to the non-linearity between the pseudorange and the receiver position, a linearization around an initial estimate must be performed. The measurement model is expressed by:


The conventional w-test method identifies one outlier each iteration, i.e., the measurement corresponding to the is excluded. In order to determine whether there are more outliers in the measurements, LS estimation is continued with the previously identified outlier excluded. Repeat until no more outliers or the number of remaining satellites is insufficient.
Limitations of the conventional W-Test
Because the conventional w-test identifies only one outlier each iteration, it is likely to cause false or missed exclusion when the test statistics are correlated. For example, suppose that there is a strong correlation between the two statistics, and only one of them has a gross error. The other statistic is likely to exceed the threshold and excluded by the RAIM technique. But the real outlier is left. Finally, after several iterations, the solution of the LS estimation is biased and the real outliers cannot be identified, resulting in a large positioning error. The correlation between the statistics is proportional to the number and the magnitude of outliers[1].
Thus, separability check is proposed in order to use w-test method for multiple outliers. The separability check calculates the correlation coefficients for every two satellites, and then those coefficients are considered when fault detection[1,2,9]. The correlation coefficient between two satellites is calculated as follows

Extended RAIM technique for multiple outliers
In the current literatures, the RAIM techniques based on w-test method for multiple outliers concentrate on the processing of residual correlation, but still identify only one outlier at a time. Thus, when the residuals are correlated, the first iteration may exclude a good observation and adversely affect the subsequent iterations. For this reason, the conventional w-test method is improved and the forward-backward method is adopted to recover the observations wrongly excluded as much as possible.
If the global test does not pass, the extended w-test method identifies two outliers instead of one at a time when local test is performed. The test statistic corresponding to the ith and jth satellite is
![]()

Separability check of the residuals is then executed according to (8). For each satellite that has identified, find the one with the highest correlation among the remaining satellites. If the correlation coefficient exceeds a certain threshold, this satellite is also flagged as an outlier. Therefore, up to four outliers can be identified each iteration. Repeat until no more outliers or the number of remaining satellites is insufficient. The initial outlier-free constellation and initial position information is obtained at the end of the forward process.
In the backward process, each flagged outlier is reintroduced. The LS estimation is no longer carried out and the initial position is used to calculate the pseudorange residual of each flagged outlier to determine whether to recover it. Since the matrix operation is involved in the LS estimation, calculation of residuals can simplify the algorithm. The residual of one satellite is calculated as follows
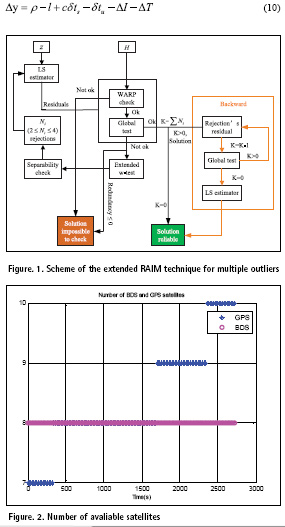

The extended technique procedure can be outlined as follows:
1) Execute LS estimation using m observations and compute the test statistic according to (9);
2) The two observations corresponding to the maximum statistic are flagged as outliers;
3) Execute separability check according to (8).For each of the two flagged outliers, if the maximum coefficient exceeds the threshold, the corresponding observation is also flagged as an outlier. Assume the number of outliers flagged by this iteration is Ni (2≤Ni ≤4);
4) Exclude the flagged outliers from the current observations;
5) Repeat 1) ~ 4) until the global test is passed and obtain the initial outlier-free constellation and the initial position information. Denote the total times of iteration as t and the number of initial outlier-free observations as OF, then OF=m–N1–N2 –…– Nt ;
6) Compute the residual of each flagged outlier according to (10) and the test statistic according to (11) and (4). If the global test is passed, this outlier is recovered as a good observation. Denote the total number of the recovered observations as RE;
7) Obtain the final outlier-free constellation which has OF+RE observations. LS estimation is performed using these observations as the final fixed solution.
Simulation analysis
A dual-system receiver produced by our institute which can process GPS L1 and BDS B1 signals is used to collect original measurements. A static test of about 45 minutes was carried out. The antenna was located on the roof of our laboratory building. The performance of the conventional and extended technique is compared by post processing. During the test period, the number of visible satellites is shown in Fig. 2.
In order to investigate the adaptability of the RAIM techniques, an error whose value is 60 meters is added to the different satellites’ pseudorange at different time. Certain satellites are assumed to be outliers at the 908sec and 1908sec respectively. The specific scenarios are shown in table I.
In the table, ‘B’ represents BDS and ‘G’ represents GPS. ‘B’ or ‘G’ is followed by the PRN number of the satellite. When the single outlier and double outliers are investigated, the navigation mode of the receiver is set to BDS. But the navigation mode is set to BDS + GPS when 7 outliers is investigated since single BDS cannot identify so many outliers.
In the scenario of single outlier, the conventional technique can identify the outlier correctly at the first iteration, indicating that the conventional technique works perfectly for single outlier. The detection process of the extended technique is shown in table II. The satellite in parentheses is the outlier flagged by the separability check, and ‘0’ indicates that there is no satellite which has a correlation with the identified outlier.
In the scenario of double outliers, the detection process of the conventional technique is shown in table III. As can be seen from table III, because the conventional w-test method only identifies one outlier at a time, the good observation is wrongly excluded at the first iteration. After removing the good observation, the weight of the real outliers is improved, this further causes wrong detection at the subsequent iteration. The navigation solution is finally biased and has a large error.
The detection process of the extended technique is shown in table IV. As can be seen from table IV, since the extended technique identifies two outliers at a time, the real outliers are identified correctly at the first iteration. The good observation having a strong correlation with the real outliers is also flagged by the separability check, but it is recovered in the backward process.
In the scenario of 7 outliers, the detection process of the conventional technique is shown in table V. table V shows that, the conventional technique can only correctly identify BDS outliers at the 908s. Both of BDS and GPS outliers are wrongly indentified at the 1908s.
The detection process of the extended technique is shown in table VI.
As shown in Fig. 2 and table VI, the extended technique can correctly identify all the 7 outliers when the number of satellites is 16 or 17. Comparing table VI with table V, it indicates that the iteration times of the extended technique is less than that of the conventional technique.
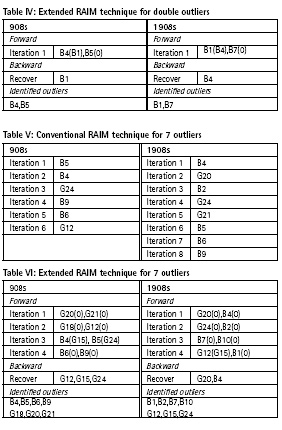
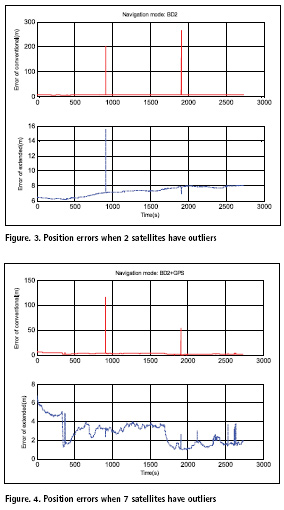
The position errors of the two techniques in the scenario of double outliers and 7outliers are shown in Fig.3 and Fig.4 respectively. In these two scenarios, the conventional technique excludes the good observations and leaves the real outliers, resulting in a larger positioning error. However the extended technique is able to correctly identify the outliers, making the positioning error relatively small. Since the number of satellites is reduced after the outliers are removed, the positioning error at the test time is slightly larger than that of the other moments.
Conclusion
RAIM is an essential part of the modern GNSS receivers and its performance plays a central role in extending the range of application for receivers. The conventional RAIM techniques which are based on single outlier assumption show failure for multiple outliers.
In the paper, the conventional w-test method is improved to make it adequate for multiple outliers. The extended technique indentifies two outliers at a time and separability check is executed to avoid missed or false detection when the statistics are highly correlated. Since up to four outliers are identified each iteration, the forward process can be accelerated. In the backward process, only the residual of each flagged outlier is calculated without LS estimation, and the amount of computation is further reduced. Simulation results show that the extended technique can effectively identify single outlier and multiple outliers, and the reliability and efficiency of RAIM is improved.
When the navigation solution is badly shifted by the outliers, it will cause good observations to appear as the outliers. Upon removal of these false detections the remaining residuals show better self-consistence. In this case, all RAIM techniques based on residual consistency and global test will fail. Future work will study the mechanism of this problem and how to solve it.
References
1) S. Hewitson and J. Wang, “GNSS Receiver Autonomous Integrity Monitoring (RAIM) for multiple outliers,” GPS Solutions, vol. 10, no. 3, pp. 155-170, 2006.
2) A. Angrisano, C. Gioia, S. Gaglione, and G. del Core, “GNSS reliability testing in signal-degraded scenario,” International Journal of Navigation and Observation, vol. 2013, Article ID 870365, 12 pages, 2013.
3) J. Ni, Y. Zhu and W. Guo, “An improved RAIM scheme for processing multiple outliers in GNSS,” Advanced Information Networking and Applications Workshops, pp. 840-845, 2007.
4) Q. Zhang, X. Zhang and X. Chang, “New method for satellite navigation identifying simultaneous multifaulty satellites,” Acta Aeronautica et Astronautica Sinica, vol. 29, no. 5, pp. 1239-1244, Sept. 2008.
5) L. Zhao, L. Li, J. Cheng and S. Luo, “New RAIM algorithm for identifying simultaneous double-faulty satellites,” Journal of Beijing University of Aeronautics and Astronautics, vo1. 36, no. 11, pp. 1261-1265, Nov. 2010.
6) I. Martini and G. W. Hein, “An integrity monitoring technique for multiple failures detection,” Position, Location and Navigation Symposium, IEEE/ION, pp. 450-467, 2006.
7) X. Zhang, X. Cui and Z. Feng. “Multiple failure detection based on reconstruction of the pseudorange error,” J Tsinghua Univ(Sci & Technol), vol. 54, no. 4, pp.425-431, 2014.
8) C. Chen and X. Zhang, “Novel method of multiplesatellite faults exclusion for global navigation satellite system,” Journal of Beijing University of Aeronautics and Astronautics, vol. 37, no. 12, pp. 1480-1483, Dec. 2011.
9) A. Innac, M. Z. H. Bhuiyan, S. Soderholm, H. Kuusniemi and S. Gaglione, “Reliability testing for multiple GNSS measurement outlier detection,” 2016 European Navigation Conference (ENC), 2016.
10) H. Jin and H. Zhang, “Failure detection using optimal parity vector sensitive to special sensor failure,” Conference on Multisensor Fusion and Integration for ntelligent Systems, pp. 55-61, 1996.












 (No Ratings Yet)
(No Ratings Yet)




Leave your response!