GPS/GNSS signals multipath modeling

GPS ranging is based on the reception of the LoS component of the signals transmitted from the constellation of GPS satellite vehicles (SV), and on measuring the time elapsed in the propagation of appropriately time-marked signal signatures. Even in the absence of any reflected (multipath) signal components, the determination of physical separations between SVs and receiver is tied to a subtlety arising from the relative motion between the two –Doppler effect. The Doppler effect can be approximately represented by a shift of the transmitted signal spectrum toward higher or lower frequencies along with an increase or decrease in the modulation (code) signal bandwidth, respectively for the cases when transmitter and receiver are approaching or receding from each other.

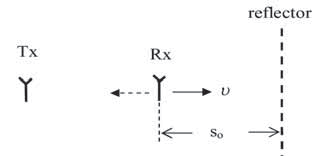
By the process of demodulation routinely performed in GPS receivers, the motioninduced spectral shifting is essentially compensated for, and the (remaining uncompensated) correlation peak positions tracked by Delay-Lock Loop (DLL) can be directly related to physical distance(s). The latter is done by multiplying the pertaining time delay by the speed of light, c, apart from correcting for ionosphere & troposphere propagation effects, clock corrections, and along with accounting for the navigation solution related SVs ephemeredes, earth rotation, etc.

Fig 1 – Mobility scenario I – fi xed refl ector and transmitter.

Fig 2–Mobility scenario II – fi xed receiver and transmitter, and moving refl ector.

Fig 3a – A situation where LoS component is tracked.

Fig 3b – A situation with refl ected component tracked.
Without such Doppler correction/tracking, the measured propagation delay would differ from the actual physical separation (say, at the time of transmission) by the group delay accumulated during the pertaining signal (energy) transition time. This in turn suggests that at every time instant the total measured delay based on Doppler shift uncompensated signal correlation peaks, or on the ranging signal markers, equals the algebraic sum of the physical delay (always positive), and the group delay accumulated up to the time of reception, which can be positive or negative, depending on the sense of relative motion. This can be described implicitly by the so-called ‘code ranging formula’
, (1)
where R₀ is the physical delay at the moment of sending, υ_r- the relative speed, and T₀ the signal transition time; Explicitly, it may be expressed by the two delay terms summation as
, (2)
with the group delay term defined by(t)=υ_r/c/t, and taking negative υr values for lowering separation distances. The presence of the time-varying group delay term of this form in (2), the socalled code Doppler, can be proven by first representing the carrier modulating base-band (code) signal g(t) in the transmit signal s(t) =g(t) sin (ω_ct) by its inverse Fourier transform components, shifting all the resulting frequency components by Doppler factor 1+ξ₀ (=1+ υ_r /c), and converting back to time-domain to get the received signal s⁰ (t) = g (t–τ(t)) sin (ω^ο_c t), with ω^ο_c = ω_c (1+ξ₀) being the Doppler shifted carrier (angular) frequency. Based on this, the Doppler uncompensated LoS signal model has the form
, (3)

where α₀ is the level scaling (normalized α₀ =1,), the relative delay Δτ₀ = 0, γ is the time-varying (physical) delay of the originally sent signal (LoS component), ω₀^D – the LoS carrier Doppler shift, and φ’ = − (ω_c + ω₀^D ) γ +φ (with φ the initial phase of the originally transmitted signal). The term ξ₀ represents the LoS component Doppler shift to carrier frequency ratio, ξ₀ (t) = ω₀^D / ω_c , or in terms of previously used relative speed, ξ₀ (t) = υ_r (t) / c. In the Doppler compensated case, s⁰ (t) = α₀. g(t-γ (t)). exp (jΔθ₀) with Δθ_o a phase shift.

Even with the LoS component undisturbed by multipath reflections, a ‘poor’ GPS receiver design can ensue, either because the pertinent signal propagation model is not correctly interpreted (this applies to the SV constellation signals modeling as well), or because the code tracking loop is too ‘heavy-driven’ by the carrier tracking loop control signal.

As the traditional multipath modeling having been in use since the very GPS inception totally ignores the LoS relative multipath code Doppler resulting from the multipath components themselves having carrier Doppler shifts differing from the LoS one, the question is what all could be the repercussions in situations involving receiver and/or reflectors mobility?! The chance that the vehicle moving in an urban-canyon area gets directed and even ends-up ‘into a ditch’, or that the aircraft shows unable to autonomously perform the Category II/III landing may be substantially increased, if one strictly follows the ‘conventional wisdom’, or de-facto ‘GPS Dogma’ that the first detectable correlation peak has to be the LoS one, or that all measured multipath delays have to be positive ‘by definition’.

Multipath modeling–static versus dynamic

Actually, in GPS/GNSS there is no such thing as an entirely static scenario. Even in the static receiver case (non-moving vehicle), in the ubiquitous presence of nearby reflectors, there is a slight (mostly sub-Hz) difference between the Doppler shifts on LoS and the reflected multipath components due to SVs motion and resulting time varying reflection angles. Still, for almost all practical purposes, except perhaps for the sub-cm accuracies, this can be considered as a static case. With low and moderate vehicle speeds of some tens of mi/h, depending on the time duration of reflection presence or its existence before the receiver is exposed to it, the generally un-modeled code Doppler effects can be of great importance. This is the more so since the resulting (LoS-relative) multipath carrier Doppler shifts (up to a few 100Hz) may remain insufficiently attenuated by coherent correlations, which due to practical implementation constraints may not be much longer than 20ms.

Traditionally, even for dynamical situations, the multipath is modeled through just the modification of the signal’s complex envelope in the (LoS Doppler corrected) form
, (4)
where α_m is the multipath component scaling ( α₀ = 1), Δτ_m is the (time varying) physical delay of the m-th component with respect to the LoS ( Δτ₀ = 0), and Δθ_m is the phase shift term induced by the reflector and the combined effect of delay and carrier frequency. Consequently, only physical delays and mostly, with some exceptions, even same carrier frequencies (Dopplers) for the LoS and the reflected paths are assumed.

If, for example, the LoS component is fully attenuated, and there exists only one reflected component with the level sufficient to allow for signal acquisition and subsequent tracking, the signal would be ‘regularly’ demodulated by the reflected signal Doppler frequency, and consequently the measured code delay would correspond to the total (presumable LoS, plus relative reflection) physical delay. Apart from the wrong delay and Doppler measurements, there would essentially be no added delay from the code delay accumulation. However, if the LoS is present with its nominal level, and the receiver keeps acquiring and tracking it, the remaining Doppler on the reflected components stays uncompensated, and the corresponding multipath correlation peaks exhibit additional group delay terms in addition to their relative physical delay terms, Δτm, or the τ_physical term, as per (2) & (3). Consequently, the multipath modeling in environments with a moving receiver and/or reflectors takes the form

, (5)
In addition to previously introduced variables in the above expression, ω_m^D is Doppler shift on the m-th signal component, φ’ = – (ω_c + ω₀^D ) γ + φ (with φ the initial phase of the originally transmitted signal), and the term ξm represents the m-th component Doppler shift to carrier frequency ratio, ξ_m(t) = ω_m^D (t) / ω_c Together with the m-th reflector LoS relative physical delay term Δτ_m, the latter defines the total delay of the m-th received signal component as Δτ_m^total (t) Δτ_m (t) – ξ_m (t).t

This analysis suggests that the codephase terms should be explicitly modeled in software and hardware simulators for each separate path (or delay-line tap) in accordance with the corresponding Doppler shift. The parameters’ dynamics should be inferred from measurements carefully conducted to capture this effect in a number of typical scenarios.

Evaluation in simple two-path scenarios

For the sake of illustration, we evaluate the underlying Doppler to code-phase conversion using the total measured delay of the reflected component with respect to the LoS, a part of which is the group delay in equation 2. The simplified scenarios are shown in Fig. 1 and Fig. 2, with s_o the separation at t = 0. To relate these to the model in (3), here m=1, and transmitter is assumed to be fixed. The received signal consists of a sum of LoS and the reflected component
,(6)
with ω₀ = ω_c (1 ––c/υ), ω’₀ = ω_c (1 +c/υ), where ƒ = ωc / 2π is nominal carrier frequency, and the total code phase shift is given by the sum of physical and group delays
, (7)
with
, (8)
and
, (9)
φ in (6) is the relative phase shift, w.r.t. the presumably tracked LoS carrier component ( ω₀ here), induced by the time delay component, and is irrelevant for code delay considerations. At t = 0, when the receiver ‘starts’ moving towards reflector, the physical delay is t _physical (0) = –2s0/c =τ₀, s₀ initial separation, and the group (code) delay is equal to zero. On the other end, after t = T = s₀ / υ, when the receiver reaches the reflector, the total (measured) code delay is given by
, (10)
and in the case of the receiver moving away from the reflector, it is given by
. (11)
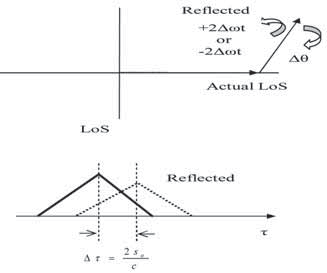
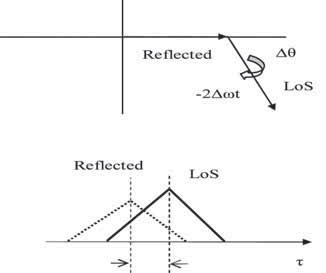
This suggests that the LoS ‘barrier’ gets‘ broken-through’, and consequently the reflected component comes ahead of the LoS one. In this simplified scenario the advancing of the reflected code correlation peak over the LoS one starts after the initial physical separation is halved, at t = T / 2, when the LoS and the reflected peak positions coincide. Essentially, this effect takes place at all relative vehicle speeds, so that it is in fact the product of relative Doppler shifts and the duration of the receiver exposure to the reflected, ie the ‘deformed’ field, that determines the actual departure of measured code phase with respect to the LoS component’s code phase. Of course, this is by no means in violation of the currently valid physical principles – we are not talking here about the electromagnetic energy propagation, but rather its group propagation, and it is a well known fact of physics that the light group speed of propagation can be measured as either higher or lower, and even negative w.r.t the speed of light propagation constant c, depending on the dispersivity features of the transmission medium. To provide some quantitative indications for the possibility that the reflected path correlation peak position itself can ‘breakthrough’ the LoS ‘barrier’, the following examples are given: For a medium dynamical situation take υ = 50km/h, S0 =15m, τ₀ = 0.1/us, and T =1.08s; these values produce 0.1/us of maximal code advance, i.e 0.4/us of maximal total code delay, respectively in cases when the receiver is moving toward reflector, and away from it. In the case of only a 10ms long coherent integration, the resulting constant Doppler shift (w.r.t. LoS) of 146Hz results in only up to 13.3 dB of the sin(x)/x attenuation. For a low mobility scenario – υ = 6.5km/h, s₀=75m, τ₀ = 0.5/us, and T=40s produce the respective maximal code advances and retardations of 0.5/us 1.5/us, the related correlation peaks remaining essentially un-attenuated (1dB at 13.5Hz) even with the coherent
integration interval time as long as 50ms. In these scenarios the maximal negative delay happens at the instant when the vehicle ‘hits’ the reflector; while for an experimental set-up this could still be feasible, in a practical situation the reflector can actually be ‘nearby-passed’, or ‘nearby-passing. Typical real-life situations of this kind would be reflections from vehicles moving in the opposite direction, and aircraft landing, for example. Relative Doppler and code phase relationships between the LoS and the reflected signal components can similarly be evaluated in the case of a fixed receiver position and a moving reflector. Although the relative speed between LoS and reflected path is the same, a very important distinction here is that the accumulated code phase difference may be fully independent of the duration of the receiver’s exposure to the reflected signal field, but may rather depend on the time interval over which at a particular location the (compressed or dilated) reflected electromagnetic field had been ‘taking place’, no matter how short the receiver exposure to the reflected signal electromagnetic field might be, provided it is long enough to reliably measure the pertinent code phase. The corresponding scenario is shown in the figure 2.

The received signal again consists of a sum of LoS and reflected components in (6),
with.

Repercussions on receiver operations

Following the acquisition of the LoS component in the figure 1 example, the tracking process can be described by the phasor diagram of Fig. 3a, with the reflected path’s phasor moving by ( ± 2Δ ωt ( Δω is the LoS relative Doppler shift) around the (ideally) zero-phase (in PLLcase) actual LoS component. Half way to the reflector, the reflected component may take control over both tracking loops. When the reflector is reached by the receiver, the tracking situation is described by Fig. 3b – with LoS now rotating over the reflected signal’s phasor. In various situations involving accelerations and highly timevarying ratios of the LoS and reflected components’ levels, the dynamics and stability of tracking loops may be affected in many diverse ways. The use of an enhanced multipath model of the kind proposed here is important for the acquisition and tracking strategies and designing effective multipath mitigation algorithms for operations in urbancanyon environments, pedestrian and jogging applications, avionics, guided weaponry, miniature autonomous systems, and other dynamical environments.

In summary

This article presented some considerations regarding a due extension and enhancement of the traditional modeling of multipath in Urban-Canyons and other dynamical environments containing Doppler shifts on reflected signal components that are generally different from the LoS Doppler. An extended model has been derived and some simple illustrative scenarios have been evaluated. The impact of the code group delays on GPS/GNSS receiver tracking loops has been discussed in qualitative terms.
An adaptation of the paper presented at the International Symposium on GPS/GNSS, November 11-14, 2008, Tokyo; and also can be found in the Proceedings of the IEEE Aerospace Conference, March 7-14, 2009, Big Sky, Montana, U.S.A.