| GNSS | |
Galileo E5 signal acquisition strategies
|
||||
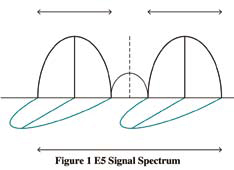
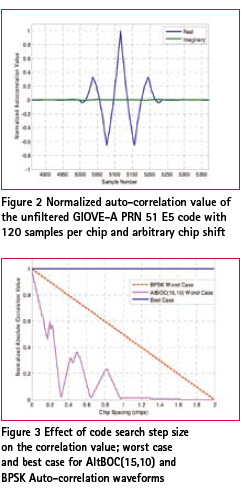
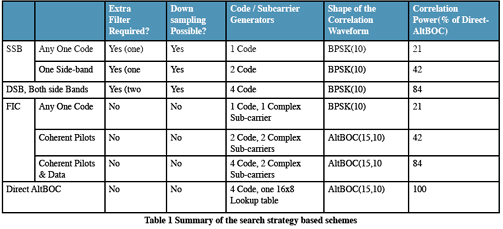
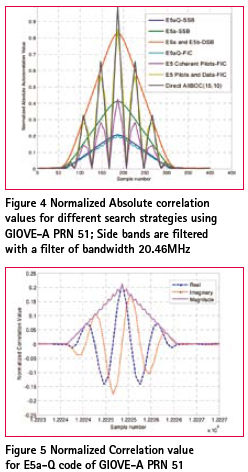
The Galileo E5 signal employs a complex sub-carrier modulation known as AltBOC(15,10) modulation. The sub-carriers are specially chosen waveforms that result in a split spectrum and a constant envelope after the modulation. Four codes are combined with these specially chosen complex sub-carriers to obtain the modulating signal which then phase modulates the E5 carrier. Alternatively, the complete modulation can be seen as an 8-PSK modulation [4, 5, 6]. The spectrum is shown in Figure 1. The transmitted signal requires a bandwidth of 51.15MHz to include the two main lobes, giving E5 the largest bandwidth of any GNSS signal. A direct method to process the E5 signal at the receiver uses the entire 51.15MHz bandwidth and performs the correlation with the locally generated replica. This results in a correlation waveform as shown in Figure 2. The correlation waveform possesses side peaks along with a sharp main central correlation triangle. The side peaks can result in ambiguous signal acquisition. Acquisition complexity and the effect of code search step sizeConcerns for the E5 signal acquisition include: • The bandwidth requirement of 51.15MHz imposes a limitation on the minimum sampling frequency and is much higher than that required by other GNSS signals. Typical sampling frequencies = 122.76MHz have been used (see [1]) • The sharp main peak in the auto correlation function requires a code search step size reduction which increases the number of cells to search during the acquisition as with the case of BOC signals [7]. • The side peaks of the auto correlation function pose the potential problem of false transition to the tracking process For the AltBOC(15,10) signal, the effect of code search step size on the correlation value is shown in Figure 5. The best case and the worst case detected signal strength are chosen to obtain an insight into the sharpness of the main peak and the effect of the side peaks [10]. For BPSK the worst case correlation value follows a linear degradation with increasing step size, as expected with a symmetrical triangular correlation function. For the AltBOC(15,10) case, not only is the degradation more steep, but there are also nulls produced by the regularly spaced autocorrelation nulls between side peaks. A typical code search step size of 0.5 experiences a loss of up to 8.8 dB relative to the best case and up to 6.3 dB loss compared to a BPSK correlation waveform with the same search step. As an example of calculating the number of search cells, consider a one millisecond pre-detection integration period which is the length of a primary code of E5. For the same worst case correlation loss as the BPSK case of 2.5 dB (code search step size of 0.5 chips) , we need to set the step size to about 0.083 chips for AltBOC(15,10). This results in 10230*(1/0.083) ~= 122760 search cells, the same as the number of samples in one millisecond assuming a typical sampling frequency of 122.76 MHz. Search strategy based techniques for acquisitionBecause of the split spectrum properties of AltBOC signals, individual signals can be acquired by independently processing the main lobes. Different acquisition approaches have been studied in [1, 8]. (1) Single Side-Band Acquisition (SSB) i. E5a-Q only or E5b-Q only ii. {E5a-Q, E5a-I} or {E5b-Q, E5b-I} (2) Double Side-Band Acquisition (DSB) i. E5a-Q and E5b-Q ii. Non coherent combination of {E5a-Q, E5a-I} and {E5b-Q, E5b-I} (3) Full-band Independent Code Acquisition (FIC) i. Any of the E5a-Q, E5b-Q, E5a-I and E5b-I ii. Coherent combination of {E5a-Q, E5b-Q} or {E5a-I, E5b-I} iii. Non coherent combination of I channels and Q channels of ii) iv. Non coherent combination of E5a channel and E5b channel (4) Direct AltBOC Acquisition i. 8-PSK like processing The Direct AltBOC Acquisition method makes use of the 8-PSK principle and the local replica can be generated using a look-up table method [5, 6]. Only the direct AltBOC approach provides the complete received power. Table 1 summarizes the search strategy based acquisition approaches discussed so far. Correlation scheme based techniques for acquisitionFigure 4 shows the correlation waveforms for some of the approaches mentioned above. Another class of acquisition technique proposed in the literature addresses the problem of side peak ambiguity in BOC signals [2, 3]. These techniques concentrate on the correlation function and try to synthesize a correlation waveform without strong side peaks. Some of the related techniques are (1) ‘BPSK-like’ method proposed in [9] and modified in [3] (2) Sub Carrier Phase Cancellation Method (SCPC) proposed in [2] (3) Very Early + Prompt (|VE2+P2|) method mentioned in [2] The SCPC method is based on the idea of removing the sub-carrier from the received signal (after carrier removal). The correlation process FIC approach works on the basis of the SCPC method. Figure 5 shows the E5a-Q correlation waveform. The SCPC method is not directly applicable to process the complete AltBOC signal since all the orthogonal components of the subcarrier and the carrier have already been used to combine the four codes. The |VE2+P2| method works on the basis that if magnitudes of two correlation values of the BOC signal separated by an appropriate delay are combined, then it results in a correlation waveform whose shape is similar to the BPSK triangle. In the |VE2+P2| method the local replica is generated as follows [2].
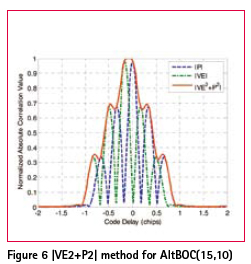
For AltBOC(15,10) signal, the delay is 0.167 chips. The resulting correlation waveform with this method is shown in Figure 6. Observe that the shape is similar to a BPSK triangle and also the peak is flat across 0.167 chips. |
||||
Nagaraj C Shivaramaiah, Andrew G Dempster
|
|||||||||||||||||||||
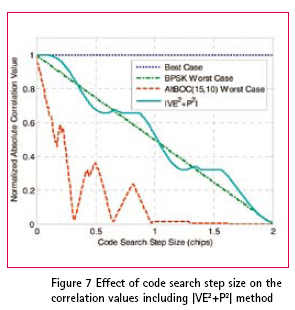
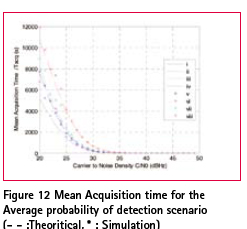
| We will now analyse the effect of code search step size with the |VE2+P2| method, see Figure 7. The worst case correlation values for the |VE2+P2| method are close to that of BPSK worst case values and swings around it. For 0.5 step size we incur only about 1 dB loss compared to BPSK worst case. A keen observation of the |VE2+P2| worst case loss curve shows us an interesting phenomenon. The curve shows flattened response at three places. The middle one is worth closely observing. From 0.5 to around 0.8 step size, the correlation loss remains at 0.67. This means that even at 0.8 step size we will incur only a loss of 3.5 dB and this loss is less than even the BPSK worst case at 0.8 step size.
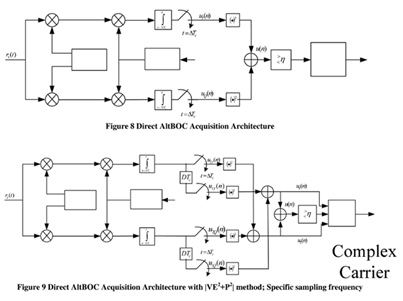
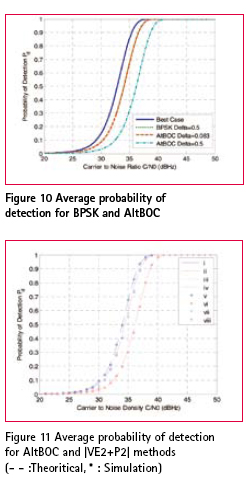
To understand the advantage in terms of number of cell searches we again consider a one millisecond pre-detection integration period. With 0.8 step size, we need only 10230*(1/0.8) = 12788 cells in the first step and around 36 cells (assuming 3 chip ambiguity and 1/12 chip step) in the second step. This is a huge reduction in the number of cells to search for the acquisition (which requires 0.1 chip step for the same loss with Direct AltBOC). When compared to the 0.5 chip stepping case which requires 20460 cell searches, we obtain an improvement of about 37%. System descriptionIn this section we describe the acquisition engine architecture to realize the Direct AltBOC acquisition and the |VE2+P2| methods. Figure 8 shows the Direct AltBOC acquisition architecture. is the code search step size used for stepping the energy search. As discussed earlier this value is typically 0.083 chips. Once the decision is made, the control is handed over directly to the tracking process. Figure 9 shows the architecture with addition of VE and P correlation values when the sampling frequency is such that it enables us to provide the required code delay D between the samples used for the addition. This is the case with sampling frequency of 122.76 MHz which can be used to realize the required D = 0.167 chips (every alternate sample). Observe that the architecture does not use any additional correlators compared to the previous approach. Also note that can be as large as 0.8 as discussed earlier. Probability of detection and mean acquisition time evaluationFigure 10 shows the average probability of detection for BPSK and AltBOC. Note that the difference between AltBOC =0.5 and the BPSK =0.5 reduces to around 2.2 dB in this case. Figures 11 and 12 provide the theoretical and simulated average probability of detection and corresponding mean acquisition time for the |VE2+P2| method with both =0.5 and 0.8 scenarios. We can see that the average probability of detection for the |VE2+P2| method is worse by 0.4 dB compared to the BPSK case and the |VE2+P2| method outperforms the Direct AltBOC approach by about 2.2 dB. Also, observe that the mean acquisition time for the |VE2+P2| method with =0.8 chip step performs better than the BPSK case with =0.5 at a given C/N0. Legends for Figures 11 and 12: i. BPSK theoretical, ii. AltBOC =0.5 theoretical, iii. |VE2+P2| =0.5 theoretical, iv. |VE2+P2| =0.8 theoretical, v. BPSK simulation, vi. AltBOC =0.5 simulation, vii. |VE2+P2| =0.5 simulation, viii. |VE2+P2| =0.8 simulation. ConclusionIn this paper we discussed the complexity and problems with the Galileo E5 signal acquisition and revisited different strategies which address these problems. We analysed the probability of detection and the mean acquisition time for these strategies especially concentrating on the |VE2+P2| method along with the acquisition engine architecture. For the same probability of detection, compared to the Direct AltBOC approach, the |VE2+P2| method results in an improvement in C/N0 of about 2.2 dB in the average scenario and about 5.3 dB in the worst case scenario. In addition an interesting observation shows that the correlation loss in the |VE2+P2| method remains constant for chip step sizes from 0.5 to 0.8 which, when exploited, reduces the mean acquisition time by 37%. We conclude that |VE2+P2| method is a good candidate for implementation in Galileo E5 receivers. AcknowledgementsThe authors would like to acknowledge that this research work has been carried out under the Australian Research Council (ARC) project DP0556848. References[1]. Dovis F., Mulassano P., Margaria D., “Multiresolution Acquisition Engine Tailored to the Galileo AltBOC Signals”, in Proceedings of ION GNSS 2007, September 2007. [2]. Heiries V., Roviras D., Ries L., Calmettes V., “Analysis of Non Ambiguous BOC Signal Acquisition Performance”, Proceedings of ION GNSS 2004, September 2004. [3]. Burian A., Lohan E.S., Renfors M., “BPSK-like Methods for Hybrid- Search Acquisition of Galileo Signals”, IEEE ICC’06, June 2006. [4]. Galileo Open Service Signal-In- Space Interface Control Document, GAL OS SIS ICD/D.0, Draft 0, May 23, 2006. [5]. GIOVE-A Navigation Signal- In-Space Interface Control Document, Issue 1, Revision 0, 02-03-2007. [6]. P.Ward, J.W. Betz and C.J. Hegarty, “Satellite Signal Acquisition, Tracking and Data Demodulation”, in Understanding GPS: Principles and Applications, Second Edition, E.D. Kaplan and C.J. Hegarty, Artech House, Norwood, MA, 2006. [7]. W. De Wilde, J.-M. Sleewaegen, A. Simsky, C. Vandewiele, E. Peeters, J. Grauwen, and F. Boon, “Fast signal Acquisition technology for new GPS/ Galileo Receivers” in IEEE PLANS 2006. [8]. J.-M. Sleewaegaen, W. De Wilde, and M. Hollreiser, “Galileo AltBOC Receiver”, in Proceedings of ENC GNSS 2004, Rotterdam, Holland, May 16-19, 2004. [9]. N. Martin, V. Leblond, G. Guilliotel, and V. Heiries, “BOC(x,y) Signal Acquisition Techniques and Performances”, in Proceedings of ION GPS/GNSS 2003, Portland, OR, September 9-12, 2003. [10]. Nagaraj C Shivaramaiah, Andrew G Dempster, “An Analysis of Galileo E5 Signal Acquisition Strategies”, Proceedings of the ENC GNSS 2008, Toulouse, April 23-25, France 2008. |
|||||||||||||||||||||
|
|||||||||||||||||||||
|
Pages: 1 2















 (No Ratings Yet)
(No Ratings Yet)




Leave your response!