| GNSS | |
From Galileo to Multisystem: Evolution of Integrity concept
The use of Galileo and EGNOS system as a single and augmented constellation allows us to develop the positioning algorithm and to improve the position accuracy |
|
 |
|
||||
 |
|
||||
The integrity concept, intended as a continuous control of the information broadcast by the satellites, has been introduced by the Galileo system. Though the RAIM technique represents the first example of integrity monitoring, it has the characteristic to detect only local errors, at receiver level. The integrity monitoring applied by EGNOS, instead, could be seen as the forerunner of the Galileo one. Though there are many differences in the definition of integrity of the two system, the main aim is the same for both, that is to protect the user against failure of the system, warning him in the shortest time and with the greater precision.
The integrity includes the system’s ability to supply, at the right time, reliable warnings to the user (alarm). The main problem in supplying this service is to determine which one could be considered safe, in fact it depends on the required operation in every fields of application. Traditionally the following parameters are used to define the safety of the service for a specific application:
• Alarm Limit (AL): maximum error allowed in the position domain before the alarm generation.
• Time To Alarm (TTA): time elapsed between error’s overcoming of the AL and reception of the alarm by the user receiver.
• Integrity Risk (IR): probability that the alarm is not delivered within the TTA.
Galileo integrity
The integrity concept developed in Galileo has the aim to ensure the correct position’s computation, achieved by the receiver, and provide a valid alarm to the user if the error in the position solution exceeded a fixed threshold, the Alert Limit, relative to the specific application.
The Galileo system provides three elements to preserve the user integrity:
• Signal-in-Space Accuracy (SISA): is the expectation of the errors relative to the SW’s clock and ephemerides, founded on long term observations.
• Integrity Flags (IF): is a warning relative to a satellite that is transmitting a signal with an excessive error. IF is founded on the short term observation of the clock’s variations, the ephemerides and the RF signals.
• Signal-in-Space Monitoring Accuracy (SISMA): is an estimation of the accuracy of the Signal-in-Space Error (SISE).
The user receiver judges the accuracy of the computed position solution, typically in term of Horizontal Protection Level (HPL) and Vertical Protection Level (VPL), through an estimate of the errors of the system, an estimate of the local errors and the knowledge of the number and geometry of the SWs used for the positioning algorithm. The computed Protection Level is then compared with specific Alert Limit, in order to determine the availability of the navigation service.
The error detected by the ground segment can be modeled with a zero-mean Gaussian distribution with variance
Galileo integrity risk
The evolution of the Galileo integrity concept concerns the verification of the system’s integrity. The separation between the vertical and the horizontal computation of the protection level has been united in an unique concept, or rather the user will be able to compute a probability, named Hazardous Misleading Information Probability ![]() , which will be compared with a threshold (TH).
, which will be compared with a threshold (TH).
Integrity Risk Algorithm
From the quantities listed above mentioned (SISE, SISA, SISMA, IF and TH), the user receiver can derive the integrity risk for the user position solution. This integrity risk is always computed for a given alert limit. Whenever the derived IR at the AL is larger than the allowed IR, the user equipment shall raise an alert.
The assumptions made for the derivation of the user integrity equation are summarized as follow:
• In a Faulty Free mode, the true SISE for a satellite is zero mean Gaussian distributed with standard deviation SISA.
• In general faulty satellite will be flagged Don’t Use.
• For each instance in time, one satellite of those flagged OK is considered to be faulty but not detected (Faulty Mode). The distribution for the SISE of a faulty satellite is Gaussian with expectation value TH and standard deviation SISMA.
Once the distribution of the error in the reference frame is known (Gaussian overbounding distribution with SISA and SISMA respectively), deriving the associate integrity risk is straightforward.
Therefore the error distribution for the vertical (one dimensional Gaussian distribution) and horizontal (Chi Squared distribution with two degree of freedom) cases need to be derived and the corresponding integrity risk can be easily computed by analyzing the integral for both distribution with respect to the given alert limit. Finally, the integrity risk at the alert limits HAL (Horizontal) and VAL (Vertical) are computed by adding the vertical and horizontal contribution (eq. 1).
where N is the number of satellite used for the positioning algorithm.
Multisystem integrity
With the advent of Galileo users will be provided with multiple signals coming from different satellite systems. This will improve position accuracy, because the number of satellites in view per user will be almost doubled. Moreover, the higher measurements redundancy will help to guarantee a safer position and the detection of errors. This will result also in an improved availability and in this way the requirements for more demanding flight categories can be satisfied. Therefore, it is necessary to introduce a base-line for a combined system, defining new parameters, new integrity algorithm and possible ways to combine the two independent systems.
With the term “Multisystem”, we mean the improvement of the accuracy and availability of the navigation solution using the combined Galileo and GPS signals. In this context, it is essential for the user to take advantage of the integrity information coming from both Galileo and GPS satellite constellations in order to prevent users from errors that might represent an excessive risk. The multisystem integrity algorithm has to establish a link between the two generations of GNSS, defining the relation for integrating different integrity monitoring schemes.
Galileo-Based Integrity Algorithm
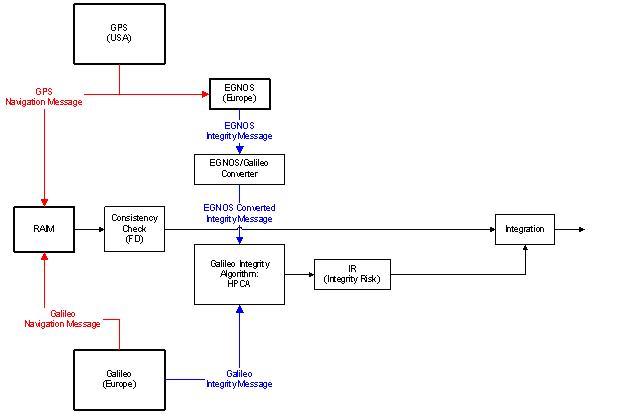
In order to define a new Integrity algorithm, for this study we have chosen an approach known as GBIA (Galileo-Based Integrity Algorithm), through which the integrity data coming from the two systems considered, Galileo and EGNOS, are implemented inside the Integrity Risk equation of Galileo.
Figure 1 shows the block diagram of a GBIA system. The fundamental block of this diagram is the EGNOS/Galileo converter, that has the aim of converting the EGNOS Integrity message into a message useable by the Galileo Integrity Algorithm.
Fig. 1 – Galileo-Based Integrity Algorithm
EGNOS is a SBAS (Satellite Based Augmentation System) that has the aim to improve the GPS system through a constellation composed by three GEO satellite and a ground segment. In EGNOS, the quality of the information is provided in the form of standard deviations related to two type of corrections, namely:
• The UDRE, that is the variance of residual clock ephemeris errors;
• The UIRE (User Ionosphere Range Error), that is the variance of residual ionospheric errors, obtained through a model based on GIVE and UIVE (User Ionospheric Vertical Error).
Hence, like in Galileo case, the error detected by the ground segment can be modeled with a zero-mean Gaussian distribution with variance:
Taking into account the different integrity allocation between the Galileo concept, that foresees the use of four failure mechanism, and the EGNOS concept, based on a failure assumption, the contribution of GPS satellite to IR computation is reduced only to the faulty free mode. Then it is possible to assume
Multisystem integrity algorithm implementation
The proposed algorithm merges integrity data originated by Galileo and EGNOS systems and employs a Receiver Autonomous Integrity (RAIM) technique (Weighted RAIM). The potentiality of this algorithm is represented by the combination of the IR algorithm with the RAIM technique. RAIM is able to detect failures not detected by the IR algorithm; in case of multiple failures, when the WRAIM technique fails, the IR algorithm triggers alarm.
The aim of this research is to enable the user to take advantage of the data transmitted by the Galileo and EGNOS systems: the user receiver must consider a single and large constellation in order to strengthen the positioning algorithm and improve the accuracy. This idea just need the definition of a new integrity concept, able to put together the techniques mentioned above.
IR equation
In EGNOS domain, IR is the probability that the horizontal (vertical) PL exceeds the horizontal (vertical) AL, without the user got any alarm. This definition asks for making a clear distinction between the horizontal and vertical case. So it is necessary to split IR in two a priori fixed quantities. On the contrary, with Galileo system, the users do not have to evaluate the horizontal and vertical protection levels, but directly the global IR without making strict allocations.
The first step on the definition of a new integrity algorithm concerning a combined constellation (Galileo+GPS), is the characterization of equivalent elements belonging to the two navigation system. In order to achieve the test on the position solution, we opted for the relationship between ![]() of Galileo and
of Galileo and ![]() of EGNOS (Section – Galileo-Based Integrity Algorithm). First of all, these are quantities defined in the same domain SIS, moreover are related to the same typology of error (clock and ephemeris).
of EGNOS (Section – Galileo-Based Integrity Algorithm). First of all, these are quantities defined in the same domain SIS, moreover are related to the same typology of error (clock and ephemeris).
The local contribution to the variance of the error in the SIS depends from the elevation angles of the satellite belonging to the two constellation considered. As mentioned before, in order to consider a single constellation composed by booth GPS and Galileo SW, we have considered the variance of the error in the SIS as follow:
![]()
where the second term represents the local error contribution.
Through a Matlab® routine we can implement the IR equation. FF and FM, in Eq.1, suggest the faulty and faulty free mode. In fact, the Galileo system assumes two separate scenarios: one in which the satellites are all set as use, and the other in which one of the satellites set as use is supposed not functioning. When you are in faulty mode, in case of Galileo satellites, the SISMA element comes out; instead, in EGNOS case, only the faulty free mode is expected and, because we could not find an equivalent for the Galileo SISMA in its navigation message, we are going to consider the following situation:
• Faulty free: for the Integrity Risk computation we consider all satellite in view, GPS and Galileo set as OK.
• Faulty mode: the involved satellite are only those belonging to the Galileo constellation, hence the index of the sum is related only to those satellites.
Inputs of the implemented algorithm
Pseudoranges are obtained by the true satellite-user distance adding a zero-mean Gaussian noise with variance depending on SISA and elevation angles of satellites.
Regarding SISA and SISMA evaluation, actual values have been considered, adding a Gaussian noise:
The matrix G is named Design Matrix and consists of the linear coefficients obtained by the partial derivatives of the observation’s equations with respect to the estimated coordinates. This matrix characterizes the user-satellite geometry. The number of the columns of G agree with the number of unknowns to be determined (X,Y,Z and b), while the rows equals the number of the available observations (number of satellites in view for both navigation systems).The union of the Galileo and the GPS constellation causes a change into the G matrix, in fact the number of unknowns became five, in order to compute the
where G and W are two matrices of dimension N x 5 and N x N respectively, with N representing the number of the satellite used in the positioning algorithm.
Receiver Autonomous Integrity Monitoring
Before going into deep in the description of the tests effected on the implemented algorithm, it is right to make an overview of the other integrity technique used in the algorithm, in parallel to the IR equation. This technique is the Weighted RAIM, that is one of the variant of the well-known RAIM.
RAIM algorithms implementation deals with multipath errors, interferences, jamming and ionospheric effects. This integrity monitoring technique strengthens the user’s protection against such local errors. The key element for the statistical test computation, inside the RAIM algorithm, is the residual error in the range domain:
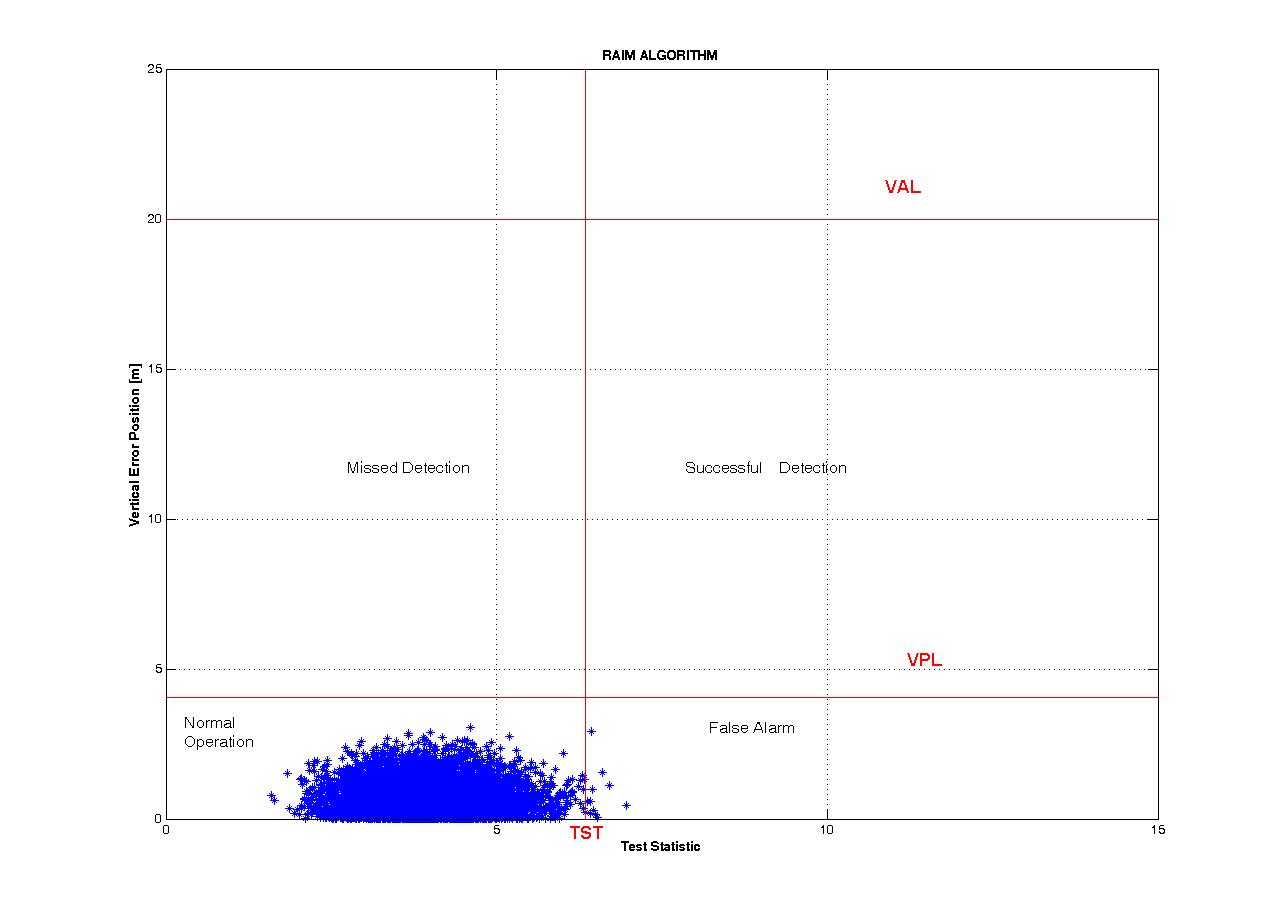
Figure 2 shows the typical representation of the distribution of operation points in the statistic vertical error plane, in a no failure conditions. The plane is divided into four regions consisting of: the normal operation points, the false alarm, the missed detection and the successful detection. The statistic is depicted by an ellipse of point that, in the case of absence of failure, is placed near the origin, instead in presence of failure the ellipse moves along a straight line, named as Vslope, towards the detection region.
Fig. 2 – Distribution of vertical error and RAIM statistic for normal operations.
Outputs of the implemented algorithm
In this Section we show the results of some simulation test organized by different typology (with or without failure) and different duration, in order to test the validity of the proposed algorithm and confirm the foreseen results.
The failure have been reproduced in two different ways:
• Introduction of a step function, at given test epoch, on the pseudo range of a satellite in view.
• Bias on SISA and SISMA.
• The step function has been chosen because it is able to characterize a lasting failure on a satellite. SISA results from predictions on satellite clock and ephemeris errors and this error’s estimations are based on long term observations: SISA increases mark out long term failures. SISA derives from a large data batch, so the anomalous behaviour of a sample is not relevant. On the other hand, pseudorange variations point out instantaneous failures.
No failure mode
In a no failure condition we are able to judge the behaviour of the new algorithm with respect to the single constellation case, and also we can evaluate the performances offered by this code in term of probability of false alarm and missed detection.
The Figure (3) illustrates the RAIM statistic in normal operation (Vertical case), without failure, showing the correct functioning of this part of the algorithm.
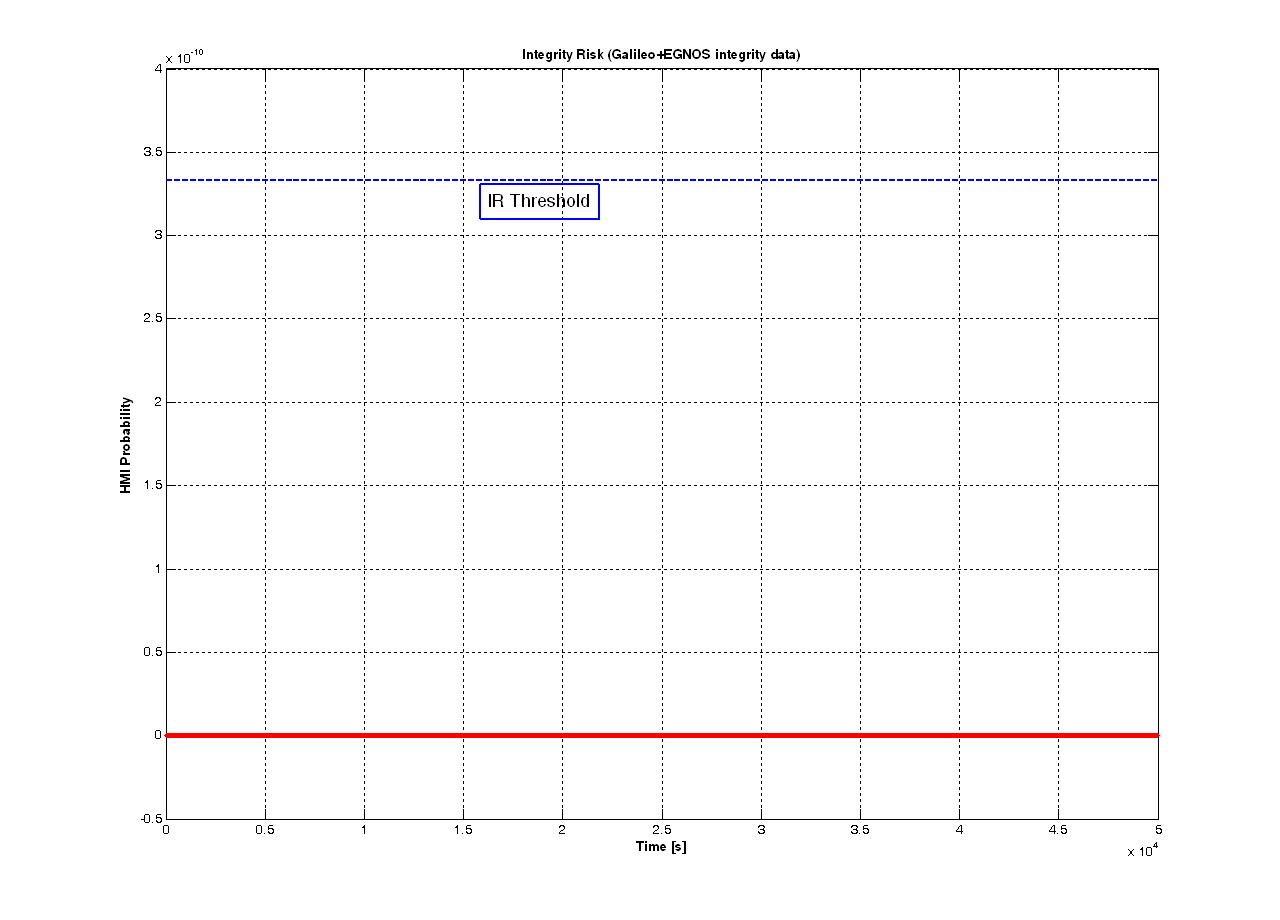
As the same we tested the IR algorithm, for the two constellation, in absence of failures (Fig. 4).
Figures 3 and 4 show that the RAIM statistic presents some samples exceeding the threshold, in particular these samples do not exceed the VPL (Vertical Protection Level). By this, we gather that the RAIM statistics presents a low probability to trigger an alarm, when it is not necessary (the main reason for this behaviour of the WRAIM could be seen in the largest sensibility to the outliers of this integrity algorithm). Instead, the IR algorithm has a lower false alarm probability than the previous case, consequence of the fact that the threshold is never exceeded and the system do not trigger any alarm when the SIS is not affected by any bias.
Fig. 3 – WRAIM in Faulty Free condition.
Fig. 4 – IR algorithm in Faulty Free condition.
Error on Pseudoranges
The local error was simulated adding a bias (fixed value) to the pseudoranges. The aim of the introduction of this bias, was to emulate the contribution of some kind of errors (i.e. multipath), that are not present in the SIS transmitted (local errors), and consequently not detectable by the ground segment of EGNOS or Galileo, but only by a RAIM technique.
Besides the noise, in order to simulate the malfunctioning in the biased case, by a certain epoch a fixed value has been added to the range measurement. Since the IR algorithm isn’t able to detect these kind of error, we show the results of the WRAIM part of the proposed algorithm for this first model of failure.
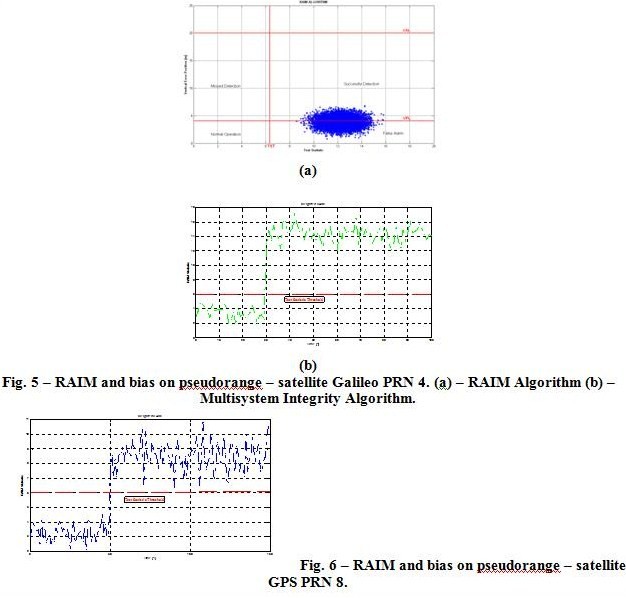
Figures 5 (b) and 6 show the istantaneous behaviour of the RAIM statistic in the presence of a bias of 20 meters inserted from the 30-th epoch in a satellite belonging to the Galileo constellation, and a bias of 10 meters, from the 50-th epoch, in a GPS satellite. In both the cases the RAIM statistic (green and blue curves) exceeds the Test Statistic Threshold with a probability of 100%. This way of representing the RAIM process is not the typical one, in fact in the example depicted in Figure 2 different sample of one epoch (the satellite configuration remains the same during the simulation, instead the noise added to the pseudoranges is varying) are considered in order to obtain an estimate of the proper functioning of the algorithm. Figure 5 (a) shows this kind of analysis made for the biased case (Galileo satellite, Vertical case); as can be seen the RAIM technique detects the error in the pseudorange, in fact the ellipse of point leaves the normal operation region exceeding the TST. The same result can be achieved also in the GPS biased case.
Error on SISA/SISMA value
The error on the signal in space has been simulated by adding a bias on the standard deviation of the noise considered in the SISA and SISMA computation of two random satellite belonging to one of the two constellation considered. In this failure mode, SISA and SISMA value have been implemented as in Eq. 7, assuming the following value for the respective standard deviation:

The following Figure (7) shows the behaviour of the implemented algorithm, in particular the IR equation, when the bias on SISA and SISMA is considered in two Galileo satellites. In this case the algorithm triggers alarms with a probability of 2%.
Fig. 7 – IR algorithm combined constellation and bias on SISA and SISMA, satellites Galileo PRN15 and PRN22.
Making a comparison with a single constellation case (only Galileo satellite), Figure 8 shows the behaviour of the Integrity Risk algorithm in Galileo case, considering the same size of bias, for the same satellite. What is clear from this comparison, is the decrease of alarms (~10%, in the second case) triggered by the system achieved by the use of the combined constellation, this means that in a dual constellation the combined system provides a safe position to the user.

Fig. 8 – Galileo IR algorithm and bias on SISA and SISMA, satellites Galileo PRN15 and PRN22.
Conclusions
The totality of the tests made on the implemented code has been planned with the aim of characterizing the performances of the algorithm respectively in faulty free and in faulty mode. The use of Galileo and EGNOS system as a single and augmented constellation allows us to develop the positioning algorithm and to improve the position accuracy. Moreover the combination of the two SVs systems leads to obtain some benefit from the RAIM point of view.
The proposed solution starts from the integrity equation defined for the Galileo system and adapts it to the combined system Galileo+EGNOS with the aim of computing the Hazardous Misleading Information Probability. We focused our attention on the IR equation: the implemented code reproduces the IR equation as is presented in literature, that is with the SISA values relative to Galileo and GPS satellites and SISMA relative only to the Galileo ones, in faulty free and faulty mode respectively. The results obtained testing the algorithm in presence of failure, have provided positive indications on the IR equation implemented: in these cases, the HMI probability increase with the value of the bias.
Though the IR protects the user against extended failure, whose effects revert on the SISE estimation, the RAIM technique, instead, could highlight instantaneous errors on the distances measured by a Galileo or a GPS satellite. RAIM and IR compensate each other, or rather the RAIM indicates failure unperceived by the IR and vice versa. This technique is based on a very different concept than protection levels and leads to different results. However, the Galileo integrity concept is more complete than GPS/SBAS and RAIM integrity concepts and offers more protection to failures. On the other hand, this concept still needs further investigations, in particular regarding the assumptions to be used for the error distributions and the parameters to be considered in the integrity equation. Indeed, although more complete, the new integrity concept introduced by Galileo is more complex and less intuitive than SBAS and RAIM protection level concept.
References
V. Oehler, F. Luongo, J. P. Boyero, R. Stalford, H. L. Trautenberg, J.Hahn, F. Amarillo, M. Crisci, B. Schalarmann, J. F. Flamand, “The Galileo Integrity Concept”, ION GNSS 17th International Technical Meeting of the Satellite Division, 21-24 Sept. 2004.
C. Pecchioni, M. Ciollaro, M. Calamia, “Combined Galileo and EGNOS Integrity Signal: a multisystem integrity algorithm”, 2nd Workshop on GNSS Signals & Signal Processing, Apr. 2007.
T. Walter and P. Enge, “Weighted RAIM for Precision Approach”, Stanford University.
P. Misra and P. Enge, “Global Positioning System, Signal, Measurements and Performance”, Ganga-Jamuna Press, 2001.
M. Ciollaro, “GNSS Multisystem Integrity for Precision Approaches in Civil Aviation”, Università degli Studi di Napoli “Federico II”, Feb. 2009.
“Galileo Integrity User Equations – Working Paper”, GAL-TNO-GLI-SYST-I/0630.
F. Luongo, V. Oehler and R. Stalford, “HPCA Input/Output Test Data”, Galileo Industries, Apr. 2004.
B. Roturier, E. Chatre and J. Ventura-Traveset, “The SBAS Integrity Concept Standardised by ICAO. Application to EGNOS”, GNSS 2001, May 2001.
J. Rife, S. Pullen, B. Pervant and P. Enge, “Paired Overbounding and Application to GPS Augmentation”, Stanford University & Illinois Institute of Technology.
ESA-DEUI-NG-TN/01331, “Galileo Integrity Concept”, issue 1, 5 July 2005.
My Coordinates |
EDITORIAL |
|
His Coordinates |
Dr Dru Smith Matthew M O’Connel |
|
Mark your calendar |
December 2010 TO AUGUST 2011 |
|
News |
INDUSTRY | LBS | GPS | GIS | REMOTE SENSING | GALILEO UPDATE |



















 (No Ratings Yet)
(No Ratings Yet)





