| Geodesy | |
Classroom Geodesy
|
|
||||||||||||
| In continuation of the discussion about the ellipsoid and geoid in the earlier interaction through the Classroom feature, let us define the reference coordinate systems. Consider a vertical axis oriented towards the north pole as Z axis. The X axis is oriented towards the First point of Aries ?. The Y axis completes a right handed system. Let ‘r’ be the unit radius of the sphere as defined in spherical astronomy. The transformation of spherical coordinates a, ß, rinto Cartesian coordinates X, Y, Z then can be defined as follows:
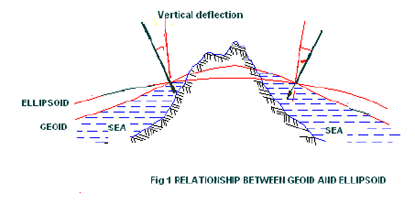
The coordinate systems for describing the satellite motion and for the position of the observation station are indeed different. One is a inertial reference system and the other is a terrestrial reference system.. Detailed description of these systems is beyond the scope of this article and the explanation of these can be found in any book on geodetic astronomy. For most practical applications ellipsoidal coordinate systems are preferred especially for horizontal coordinates in geodetic networks, because they closely approximate the earth surface. Geodetic datumThe concept of geoid and ellipsoid can better be understood through the fi gure 1. For most practical applications ellipsoidal coordinate systems are preferred especially for horizontal coordinates in geodetic networks, because they closely approximate the earth surface. The angle ? between the directions of the ellipsoidal normal and of the plumb line at point P is called the defl ection of the vertical. A global ellipsoidal system is related to reference ellipsoid system that fits the earth surface as a whole. The origin of the ellipsoid is supposed to coincide with the geocentre. The set of parameters that describe the relationship between a particular local ellipsoid and a global geodetic reference system is called geodetic datum. A geodetic datum is defi ned by a set of parameters depending upon the extent of consideration of the parameters of the ellipsoid. The most significant parameters to be considered are e, f, ? X, ? Y and ? Z. Here ‘e ’ is semi-major axis of the ellipsoid, fis flattening parameter, and ?X, ?Y and ?Z are the coordinates of the ellipsoid origin (translation parameters or datum shift parameters) with respect to the geocentre. They represent a mean position of the particular local system with respect to the geocentric system. For ? X, ? Y and ? Z equal to zero, the geodetic datum is called an absolute datum. Here the three rotation parameters are ignored. The number of the datum defi nition parameters increases when the datum information is derived from satellite orbits. In such a case the coeffi cients of earth gravity field, constants of earth rotation, geocentric gravitational constant form part of datum defi nition. WGS 84 is an example of such geodetic datum. For ? X, ? Y and ? Z equal to zero, the geodetic datum is called an absolute datum. The parameters of WGS 84 based on continuous evaluation are as follows: Flattening parameter f = 1 / 298.257223563 The period from 1980s onwards has brought useful developments in satellite geodesy. This has resulted in operational use of satellite techniques in geodesy, geodynamics and surveying. This process started with NAVSTAR GPS.
|
||||||||||||


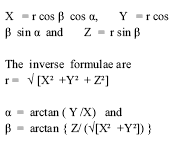











 (No Ratings Yet)
(No Ratings Yet)



