| LBS | |
Acquisition sensitivity limits of new civil GNSS signals
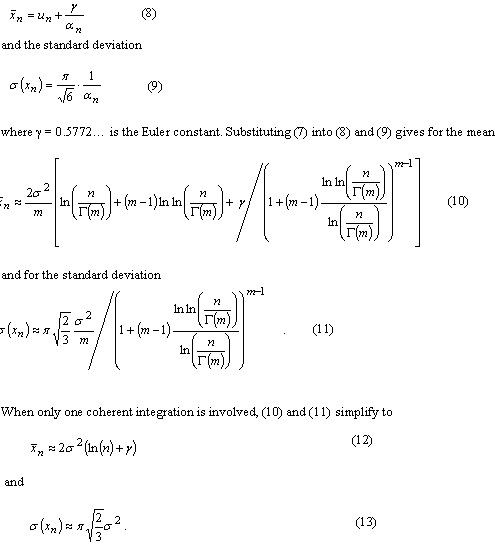
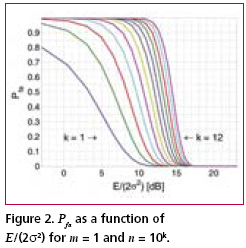
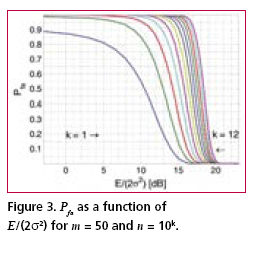
Theoretical and practical limitationsA useful insight into parallel acquisition can be gained by examining the statistics of noise bins in the search space. It is well known that the squaring and subsequent summing of m independent complex zero-mean Gaussian variables results in a central chi-square distributed variable with 2m degrees of freedom [Proakis]. This is exactly the process that produces the noise bin values when there are m coherent integrations and when the input is thermal noise. Assuming a constant total reception time and an input power that corresponds to a noise variance equal to s2 at both integrator outputs when m is one, the cdf of a noise bin for an arbitrary m is The related mean value of the distribution is Extreme value theory (EVT), a branch of mathematics developed by Fisher, Tippett, Gumbel and others during the 20th century, proves that the limiting distribution Fn of the maximum of n i.i.d. random variables, when n tends to infinity, has one of three possible functional forms depending on the tail of the parent distribution. For the chi-square distribution and other distributions with an exponentially decreasing tail, the limiting distribution has the double exponential form for the chi-square distribution can be obtained from an expression given by Gumbel [Gumbel] for the gamma distribution. Numerical evaluation shows that the approximation is fairly accurate for values of m up to five or six. Substituting (6) and (1) into (5) gives The double exponential distribution (3) has the mean value It can be seen from (10), (11), (12) and (13) that the mean of the maximum of the chi-square distributed noise bins has a logarithmic or slightly stronger than logarithmic dependency on the size of the search space, while the standard deviation of the maximum is nearly constant. In other words, the graph of the probability density function of the noise maximum maintains its width but is shifted horizontally when n changes. This means that signal detection thresholds also have to be shifted in order for error probabilities to remain constant. The consequence of this is that the receiver acquisition sensitivity is lower when the size of the signal search space is larger, the required signal power being approximately proportional to the logarithm of the size of the space. In an earlier contribution [Turunen] the author derived an expression for the false acquisition probability in a scenario where a satellite signal is known to be present and the receiver simply chooses the highest peak in the search space. With the noise power assumption made above and with a signal power such that the squarer output is equal to E when m is one, the false acquisition probability for an arbitrary m was found to be is the pdf of the non-central chi-square distribution obeyed by the signal bin. The last term in (15) is the modified Bessel function of the first kind of order m-1. Substituting (1) and (15) into (14) and making the substitution is the incomplete gamma function. |


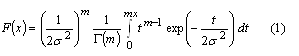
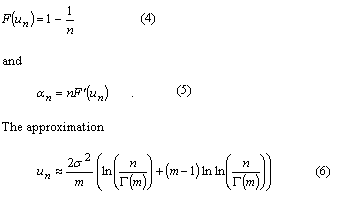
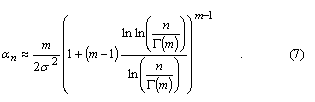
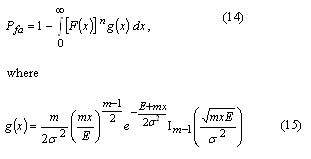
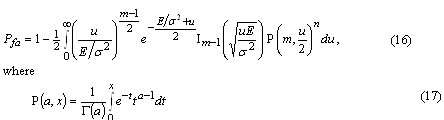










 (No Ratings Yet)
(No Ratings Yet)




