| GNSS | |
Deformation Analysis of the Territory of Bulgaria from GNSS observations
The present study is an attempt to contribute to the geokinematics of the territory of Bulgaria by means of Finite Elements Method (FEM) on the base of estimated GNSS station coordinates in different observational epochs |
 |
|
 |
|
The territory of Bulgaria is one within the Balkan Peninsula region with active tectonics and seismotectonics. A number of geodynamical investigations try to give an adequate interpretation of the obtained results (Burchfiel et al., 2006), (Kotzev et al., 2006), (Matev, 2011), (Milev, Dabovski, 2006), etc.
Global Navigation Satellite Systems (GNSS) have been recently used for geodetic observations and determination of the earth crust movements in millimetre level. Velocity vectors of located GNSS stations can be estimated and their behaviour can be analyzed. Except station behaviour also surface deformations are of interest for the earth movements of blocks or large areas.
The present study is an attempt to contribute to the geokinematics of the territory of Bulgaria by means of Finite Elements Method (FEM) on the base of estimated GNSS station coordinates in different observational epochs.
Finite elements method for space
At present the finite elements method is used successfully in the analysis of movements of stations, which are results from GNSS data processing in order to be obtained strain tensors and strain accumulation (Bogusz et al., 2013), (Deniz, Ozener, 2010), (Hu et al., 2004), (Valev, Kastreva, 2006), (Valev, Vassileva, 2000). Here this method is developed and applied for deformation analysis in the space – determination of principal deformations and their directions as an appropriate method for large territories. The finite elements (triangles) for different observational epochs are formed in such a way that they are not overlapped.

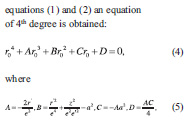
and e, e’ are the first and second eccentricity of the meridian ellipse.
The Ferrari method is the most convenient for the solution of equation (4) as it is a method for reducing the solution of an equation of degree 4 to the solution of one cubic and two quadratic equations. After solution of these equations the root ro is obtained and finally the Cartesian station coordinates (X0, Y0, Z0 ) of point P0 are calculated by
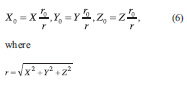
The azimuths ai,k of the ellipsoidal triangle chords (baselines) between triangle apexes i and k of the finite elements are obtained from the following relationship:

Linear deformations mi,j, mj,k, mk,i (i, j, k – triangle apexes) of respective triangle sides S, S’ between two observation epochs t and t’ are calculated as follows:

Finally, the linear deformations m of the triangle sides are obtained from the following equations
![]()
Semi-axes of the ellipses of deformations a, b (Valev, 1995), (Kastreva, 2000) are obtained by use of linear deformations m of either triangle side, i.e.
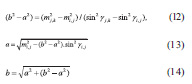
Finally the principal deformations a’ and b’ (major and minor) and their directions are determined from

GPS data processing of BULiPOS reference network
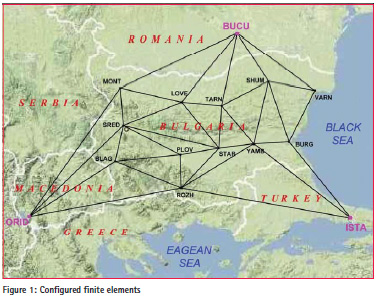
As an appropriate method for deformation analysis based on GNSS data for large territories the proposed finite elements model is applied for the territory of Bulgaria using estimated Cartesian coordinates of BULiPOS GNSS network stations (Milev et al., 2014). Stations of the BULiPOS GNSS network are shown in figure 1.
One week GPS data from each of the five years 2009 – 2013 of BULiPOS network stations have been processed with Bernese software, version 5.0. Ten IGS stations have been involved in the processing. The estimated Cartesian coordinates of the stations have been transformed in ETRF2000 by applying ETRF components of the Eurasia plate rotation pole. These relative to the Eurasia stable plate station coordinates have been used in the finite elements model.
Application of FEM for the BULiPOS reference network
The finite elements have been configured using all BULiPOS stations on the territory of Bulgaria and the nearest three IGS stations – BUCU, ISTA, ORID from all together 10 IGS stations, as it is shown in figure 1.
All together 21 finite elements (triangles) have been formed. The ETRF2000 coordinates X, Y, Z of all stations in each year have been transformed into ellipsoidal station coordinates Φ, λ, h and then they have been transformed into Cartesian station coordinates (X0, Y0, Z0) onto the ellipsoid used. The (X0, Y0, Z0) station coordinates have been used for determination of the ellipsoidal chords (baselines) between stations on the ellipsoid by formula (7), which are actually triangle sides of every finite element in each year. According to the formula (11) linear deformations of all triangle sides have been determined using obtained lengths of triangle sides from all five years in all combinations between five year’s results. Deformations of compression and extension of triangle sides obtained by formula (11) are shown in yellow colour in figure 2 for the longest time period of four years 2009-2013.
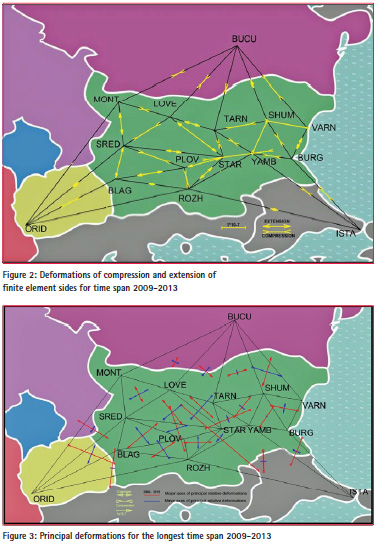
The smallest relative movements are obtained between station BUCUTARN, TARN-STAR, ORID-ROZH, ORID-MONT and ROZH-YAMB, which are between 0,005÷0,015.10- 7 and that corresponds to the extension of 0,1÷0,2mm for all the mention sides except BUCU-TARN, which is compressed. Considering the obtained results for the west part of Bulgaria where they show an extension in direction northsouth it can be concluded that there is a good agreement with the directions of estimated GPS velocities of movement from other studies (Burchfiel et al., 2006; Georgiev et al., 2011; Kotzev et al., 2008; Matev, 2011; Zagorchev, 2011) and the results confirm the belonging of south-west Bulgaria to the Aegean extensional zone. The largest relative movements are obtained between stations STAR and LOVE – extension of amount of 1,031.10-7 and between stations STAR and YAMB – compression of amount of 1,316.10-7. In fact these are 9,6mm, respectively – 11,3 mm linear deformations. For most of the finite element’s sides there is no disagreement of the obtained deformations in all time spans studied except a few of them.
Magnitudes and directions of the principal deformations of each finite element are obtained by formula (15). They are calculated for time spans 2009- 2013, 2010-2013 and 2011-2013. The magnitudes and directions of the principal deformations for the longest time span 2009-2013 are shown in figure 3.
The obtained results for the three time spans agree very well except for the finite elements including stations with very small movements (Love, Burg) and with the problematic station Varn. Deformations in north-west and in part of central Bulgaria show extension in north-south direction and compression in south-west to the north-east direction. Central-east and south-east part of the country are under compression with different directions of particular areas. The largest deformations of compression appear in central Bulgaria, close to station Star in direction north-west to south-east.
Conclusion
The finite elements model in space is applied for deformation analysis of whole territory of Bulgaria for the first time. On the base of the obtained linear deformations of finite element sides (Figure 2), their analysis and comparison it could be generalized and suggested that in northern Bulgaria (Moesia platform) there is compression, in west Bulgaria – extension with direction north-south, in central Bulgaria (Maritsa basin) – extension and in east-south Bulgaria – compression. On the base of the obtained principal deformations (Figure 3) several areas of compressions and extensions could be distinguished but not quite clear. Generally it can be suggested that deformations in part of central, central-east and southeast Bulgaria are of compression, in north-west, south-west and in part of central Bulgaria – of extension, which agree with the linear deformations. More stations over the territory of the country will contribute to better clarification of deformation processes.
Acknowledgements
We would like to thank the team of IPOS LtD for kindly provided us all necessary GNSS data for the processing.
References
Bogusz, J., A. Klos, M. Figurski, M. Jarosinski, B. Kontny, 2013. Investigation of the reliability of local strain analysis by means of the triangle modelling. Acta Geodyn. Geomater., Vol. 10, No. 3 (171), 293–305, 2013 DOI: 10.13168/AGG.2013.0029
Burchfiel, B. C., R. W. King, A., Todosov, V., Kotzev, N., Durmurdzanov, T., Serafimovski, B., Nurce, 2006. GPS results for Macedonia and its importance for the tectonics of the Southern Balkan extensional regime, Tectonophysics, 413, 239–248.
Deniz, I., H. Ozener, 2010. Estimation of strain accumulation of densification network in Northern Marmara Region, Turkey. Nat. Hazards Earth Syst. Sci., 10, 2135–2143, 2010 www.nat-hazardsearth- syst-sci.net/10/2135/2010/ doi:10.5194/nhess-10-2135-2010
Hu, Y., K. Wang, J. He, J. Klotz, G. Khazaradze, 2004. Three-dimensional viscoelastic finite element model for postseismic deformation of the great 1960 Chile earthquake. Journal of geophysical research, Vol. 109, B12403, doi:10.1029/2004JB003163, 2004 Kastreva, P., 2000. A way for defining the deformations according to the method of the final elements and its application to the geodynamic network “Krupnik”. Reports of Geodesy, Warsaw University of Technology, No 4(49), 229-233.
Kotzev, V., R. Nakov, Tz. Georgiev, B.C. Burchfiel, R.W. King, 2006. Crustal motion and strain accumulation in western Bulgaria, Tectonophysics, 413, 127–145.
Kotzev, V., R.W. King, B.C. Burchfiel, A. Todosov, B. Nurce, R. Nakov. (2008). Crustal motion and strain accumulation in the South Balkan Region Inferred from GPS Measurements, in Husebye, E., ed., Earthquake monitoring and seismic hazard mitigation in Balkan countries:
Proceedings of the NATO Advanced Research Workshop on Earthquake Monitoring and Seismic Hazard Mitigation in Balkan Countries, Borovetz, Bulgaria, 11–18 September 2005: NATO Science Series IV: Earth and Environmental Sciences. Volume 81, 19–43.
Matev, K., 2011. GPS constrains on current tectonics of southwest Bulgaria, northern Greece and Albania. Thesis, Doctor of university of Grenoble, 203pp.
Milev, G., Dabovski, C. (Eds), 2006. Geodynamics of the Balkan Peninsula, Monograph, Reports on Geodesy, Warsaw University of Technology, Institute of Geodesy and Geodetic Astronomy, 647 pp.
Milev, G., K. Vassileva, I. Milev, R. Pelovski, I. Andreev, G. Gerova, 2014. Current status and activities of Satellite Ground-Based System EUPOS and EUPOS-BG. SES 2013, Proceedings of Ninth Scientific Conference “Space, Ecology, Safety”, 163-173. Valev, G., 1987. Projection of points onto the earth ellipsoid. Geodesy, Cartography and Land Management, 4, 6-11. (in bulg.)
Valev, G., 1995. Another approach to derive the parameters of the ellipse of deformations. Geodesy, Cartography and Land Management, 2-3, 15-19 (in bulg.) Valev, G., P. Kastreva, 2006. Stress strain analysis of the Balkan Peninsula. Balkan Peninsula monograph, Reports on Geodesy, Warsaw University of Technology, No 5(80), 2006, 597-605.
Valev G., K. Vassileva, 2000. Application of Different Models of Adjustment to the Processing of Geodetic Measurements on Geodynamic Poligons. Reports of Geodesy, Warsaw University of Technology, No 4(49), 219-227.
Zagorchev, I. (2011). Cenozoic Block Rotations in the Balkan Peninsula. Proceedings of 3rd International Symposium of the Black Sea region, 1-10 October, 2011, Bucharest, Romania, 220-222.













 (7 votes, average: 2.43 out of 5)
(7 votes, average: 2.43 out of 5)





Leave your response!