Static precise point positioning using triple-constellation GNSS

This paper evaluates the static PPP solutions using triple-constellation GNSS in seven different modes. The evaluation is done in terms of positioning accuracy, convergence time and Positional Dilution of Precision (PDOP)

Robert S B Galatiya Suya Lecturer, Geodesy and Geomatics Measurements Techniques (GMT), University of Malawi- The Polytechnic

Precise Point Positioning (PPP) is a versatile tool that has drawn attention among researchers in processing static and kinematic Global Navigation Satellite System (GNSS) datasets (Choy et al. 2013; Gao and Chen 2004; Zhang et al. 2015; Zumberge et al. 1997). PPP requires long observation period to attain a desired positioning accuracy (Bisnath and Gao 2009). To achieve ten centimetres (10 cm) or better two-dimensional (2D) positioning accuracy, PPP needs a convergence time of about 50 minutes (50 min)(Choy, Bisnath, and Rizos 2017). The convergence time of a PPP solution vary based on receiver position dynamics, observation quality, sampling rate, number and satellite vehicles (SVs) in view (Héroux et al. 2004).

The continuously changing satellite configuration in space with time compromises the PPP performance (Geng et al. 2009). The fusion of different GNSS constellations improves PPP positioning accuracy, convergence time (Cai and Gao 2013; Ceylan et al. 2015), reliability, and availability (Ge et al. 2012; Li et al. 2015). This improvement is attributed to increased number of visible satellites (Pan et al. 2017) that consequently maximises signal power-level (Shen and Gao 2006). This consequently widens the spectrum of PPP application in GNSS-denied environments (Schönemann, Becker, and Springer 2011) namely: urban canyons, heavily forested areas, and mountain valleys.

Before the modernization of Galileo and BeiDou, the integration of multi-GNSS PPP incorporated only GPS and GLONASS constellations (Melgard et al. 2009). Today, with the benefits accrued from multi-GNSS constellation, studies have been undertaken in different GNSS combinations. Lou et al. (2016) analyse the contribution of Multi-GNSS PPP solution to single and dual-frequency raw observations based on 105 MGEX stations. Pan, Chai, and Kong (2017); Zhao et al. (2017) gather improved average convergence in three-dimensional (3D) based on different combinations of GPS, GLONASS, Galileo, and BeiDou constellations. Rabbou and El-Rabbany (2015) assesses the contribution of Galileo to GPS PPP performance. Pan et al. (2017) extend the study by evaluating Galileo PDOP values on a global scale. Recently, Xia et al. (2018) carry out a similar study but by comparing the Galileo input to multi-GNSS PPP solution.

In analysing PPP with respect to conventional GNSS positioning, Soycan and Ata (2011) yield better positioning accuracy in PPP of 10 mm and 20 mm in 2D and vertical components, respectively, from one week daily observations obtained from 60 Ordinance Survey (OS) stations. In a separate study from 24-hour datasets, Soycan (2012) comes up with a better 2D positional accuracy of 6.6 mm and 9 mm in the elevation dimension with a very high precision in the north coordinates of 3.1 mm.

Furthermore, Abd-Rabbou and El- Rabbany (2017) come up with positional accuracies of 18%, 20% and 13% in dual-constellation of GPS+BDS, GPS+Galileo and in quad-GNSS PPP, respectively. Tegedor et al. (2016) yield improved results in PPP positioning and convergence time in four-system constellation of GPS, GLONAS, Galileo and BeiDou. Yu and Gao (2017b) obtain better results in triple- GNSS constellation of GPS+GLONASS+BDS from receivers on a vehicle with an improvement in PDOP values. Afifi and El- Rabbany (2016) develop a between-satellite single-difference (BSSD) undifferenced model and obtain an improvement in convergence period in triple constellation of GPS+Galileo and BeiDou. Lou et al. (2016) witness a reduction in convergence time in GPS PPP over GLONASS PPP and BDS PPP solutions in both single and dual-frequency approaches except in high altitude areas where GLONASS dual frequency PPP outperforms GPS single-frequency PPP solution. Odolinski, Teunissen, and Odijk (2014) and Abd Rabbou, El-Shazly, and Ahmed (2017) gather better improvement in convergence time in dual-constellation of GPS+Galileo than in single-system constellation of GPS-only PPP.

Triple-constellation PPP has become possible due to improvement in Galileo satellite orbit and clock products (Rizos et al. 2013). Most studies on multi-GNSS PPP do not provide a fair evaluation of different combinations of GNSS. In this study, static PPP with triple-constellation GNSS of GPS, GLONASS and Galileo is evaluated in seven combinations: GPS-only, GLONASS-only, Galileo-only, GPS+GLONASS, GPS+Galileo, GLONASS+ Galileo, and the combined PPP solution of GPS, GLONASS and Galileo. The single and combined PPP static solutions are evaluated in terms of positioning performance, convergence period and PDOP.

Multi-GNSS constellation PPP models

Basic carrier phase and pseudorange observation models

The GNSS observation models for carrier phase (L) and pseudorange (P) from the satellite (s) to the receiver (r) at carrier frequency (j) are expressed as follows:

Linearized phase and code observation models

The slant tropospheric delay is the sum of the wet and dry components and are estimated as unknown parameters (Li et al., 2013). Ionosphere-free combination observations are normally employed in PPP to mitigate the first-order ionospheric delay (Kouba and Héroux 2001; Yu and Gao 2017a). From the basic carrier phase and pseudorange observation equations [1] and [2], the associated linearized observation models are expressed as follows:

Triple-GNSS constellation PPP models

The G- and E-satellites use Code Division Multiple Access (CDMA) whereas R-satellites use Frequency Division Multiple Access (FDMA). In CDMA, each satellite transmits a Coarse/ Acquisition (C/A)-code and a Precision-code (P-code) (Kaplan, 2006).Unlike the modernised GLONASS satellites which can transmit a CDMA signal on a new L3 frequency, originally the system transmitted signals within L1 and L2 bands (Teunissen and Montenbruck 2017). Notwithstanding this, it should be mentioned that individual satellites differ in frequency and signal structure. This calls for the application of Differential Code Biases (DCBs) in order to achieve precise positioning performance.

Simplified Triple-GNSS Constellation PPP Models

Multi-GNSS constellation brings about an increased number of biases that need to be accounted for in a PPP algorithm (Schaer 2017). Even though, precise ephemeris eliminates the biases in coordinates and time, receiver and satellite hardware biases need to be accounted for (Cai and Gao 2013). The implementation of multi-GNSS DCB products alongside precise satellite orbits, clocks from IGS multi-GNSS Experiment (MGEX) becomes necessary (Montenbruck, Hauschild, and Steigenberger 2014). Equations [6] and [7] simplify to [8] and [9] when the MGEX products are implemented.

PDOP model

The tips of the receiver-satellite unit vectors form a polyhedron whose volume assists in defining DOP values. Geometric Dilution of Precision (GDOP) defines the precision and accuracy GNSS observations from satellites (Azami, Azarbad, and Sanei 2013). From Altamimi & Gross (2017), PDOP is simply the GDOP without the contribution of the receiver clock (qξ). For the sake of clarity, PDOP (σP) [13] is deduced from the diagonal elements (qx, qy and qz ) of a co-factor matrix of receiver position [12] as expressed in Leick, Rapoport, and Tatarnikov (2015):

Triple-GNSS static PPP data processing

Datasets

The MGEX stations selected in this study are illustrated in Figure 1. The selection criterion was based on the fact each of these stations tracks at least GPS, GLONASS, and Galileo satellites. In this study, one week observations were used for the year 2017 from DOY 060 to DOY 066.

Data processing parameters

Pseudorange differences corrected for ionosphere path delays are a source of DCBs for multi-GNSS constellation (Montenbruck et al. 2014). Processing Triple-GNSS constellations in different combinations utilises DCBs from MGEX provided in Bias SINEX (Solution Software/technique INdependent EXchange) format which is simply an exchange of code and phase bias information. The prototype DCBs are generated by the Center for Orbit Determination in Europe (CODE) (Prange et al., 2015); Centre National d’Etudes Spatiales (CNES) (Loyer et al. 2012); GeoForschungsZentrum Potsdam (GFZ) (Uhlemann et al., 2015; Deng et al., 2014); Technische Universität München (TUM) (Steigenberger et al. 2013); Wuhan University (Guo et al. 2016) and Japan Aerospace Exploration Agency (JAXA) are all convenient for implementation in multi-GNSS PPP algorithm. Table 1 summarises these DCBs.

Guo et al. (2017a) and Guo et al. (2017b) identify minor differences between precise ephemeris generated in analysis centres (ACs) and those provided by the Deutsches GeoForschungsZentrum (GFZ). This paper takes advantage of the DCBs computed by GFZ in evaluating the triple-GNSS static PPP performance. To thoroughly evaluate triple-GNSS static PPP performance in different combinations, a state-of-the-art GAMP was used. GAMP is a command line software capable of handling multi-constellation and multi-session data processing written by Zhou et al. (2018). Table 2 depicts the data processing parameters implemented in this study.

In this contribution, three output files from GAMP are considered: positioning root mean square error (RMSE) values, convergence time, and PDOP. The position errors are estimated with respect to a priori coordinates for the stations contained in the SINEX files from the IGS (International GNSS Service). The convergence time is estimated as the time interval from the start epoch to the convergence epoch (Xia et al. 2018). In this study, PDOP values are used to demonstrate the influence of the receiver-satellite instantaneous geometry of the visible satellites on station positioning.

Results and analysis

Positioning accuracy

The positioning RMSE values in North, East, Up and 3D for the seven (7) stations for the selected DOY are averaged and are depicted in Figure 2. The averaged RMS values for the triple PPP solution of GRE yield the best results in N, E, Up and 3D out of all the seven PPP scenarios. The statistical evaluation of the 3D positions is presented in Table 3.

The averaged PPP positioning performance was the best in GRE (11.6 cm) combination among the seven PPP solutions. The performance of dual-constellation of GR (15.4 cm) ranks second, followed by GPS-only PPP with an average of about 19.7 cm. Here, it can be seen that there was no meaningful difference between GPS-only PPP and GPS+Galileo PPP solutions. This slight difference is attributed to insufficient number of visible Galileo satellites contributed to the GPS-only PPP solution (Xia et al. 2018). For the same reason, the static PPP for Galileo was not possible for MAL2 and MOIU stations. This is indicated with zeros (0s) in Table 3.

Furthermore, the combined solution of GE falls on the fourth of the seven different combinations with an average of 19.8 cm. The GLONASSonly (31.6 cm), Galileo-only (61.9 cm) and GLONASS+Galileo (105.4 cm) fall on the fifth, sixth and seventh positions, respectively in terms of positioning accuracy. The combined solution of GPS+GLONASS is necessary in cases of few visible satellites in either of them (Tolman et al. 2010; Li, Zhang, and Guo 2009).

The statistical results indicates better performance for GLONASS-only static PPP solution than that of GLONASS and Galileo combined solution. The poor static PPP solution in the GLONASS+Galileo PPP combined solution may be attributed to both reduced number of Galileo visible satellites and poor orbit and clock accuracy of Galileo (Xia et al. 2018). As can be seen in Table 3, the positioning accuracy improves with increase in number of GNSS-constellations. The averaged 3D RMS value for NKLG was the most outstanding with an improvement of 77.5% in the triple-constellation.

Convergence time

The contribution of triple-GNSS constellation to PPP performance was also evaluated in terms of convergence period. Figure 3 and Table 4 present the averaged convergence time for seven PPP scenarios. As can be seen in Figure 3 and Table 4, no Galileo satellites were tracked for MAL2 and MOIU stations. For all selected DOYs, Galileo-only PPP solution had the poorest convergence time with that of DJIG station reaching up to about eight (8) hours.

In both Figure 3 and Table 4, it is apparent that the addition of any other GNSS constellation to GPS considerably improves the convergence time. The average improvement in the dual- and triple-constellation PPP solutions is presented in square blankets (Table 4). SUTM station had the best average improvement in convergence time of about 61% (from 220.1 min to 86.0 min) in the triple-GNSS PPP solution whereas MOIU has the worst (0.7%). For this station (SUTM), the dual-GNSS constellation of GPS+GLONASS convergence period was not different from that of the triple-GNSS constellation. This may be attributed to reduced number of satellites contributed by Galileo in the three-system GNSS PPP static solution. It is noticeable that the convergence time vary for each station. However, the average convergence time is the best in the triple-GNSS PPP.

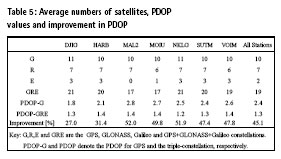
PDOP

The number of satellites, average PDOP and improvement in PDOP are presented in Figure 4. The average number of GPS satellites vary between 10 and 11 per day for the selected stations. The average number of GLONASS satellites vary between 6 and 7 per day whereas Galileo satellites in view vary between 0 and 3 as can be seen in Table 5. GNSS positioning requires at least four satellites to perform an autonomous positioning. For the selected stations, the average number of Galileo satellites are not enough for a GNSS survey.

DJIG has the least improvement in PDOP of about 27% as a result of the addition of GLONASS and Galileo satellites to GPSonly static PPP. MAL2 and NKLG station have PDOP improvements of about 52.0% (from 2.8 to 1.4) and 51.9% (from 2.5 to 1.2), respectively. The PDOP values in GPS-only static PPP improves by about 45% (from 2.4 to 1.3) for all stations. All other improvements in PDOP with respect to GPS-only static PPP are presented in Table 5. The triple-GNSS static PPP has better satellite visibility and precision factor (PDOP) than the single- GNSS system of GPS. This is indicated by much less PDOP values which are in the range of 1.2 to 1.4 in the triple-GNSS static PPP than that of GPS-only static PPP (which are in the range of 1.8 to 2.8). It can be verified that triple- GNSS static PPP can significantly improve the spatial distribution of satellite.

Conclusion

In this contribution, static PPP using tripleconstellation GNSS was assessed in terms of positioning performance, convergence time, and PDOP. GNSS observations from seven (7) MGEX stations spread over Africa were analysed for DOY 060 to DOY 066 for year 2017 in GAMP.

The observations were analysed in seven different GNSS PPP solutions. Based on the results, the following conclusion are drawn:

1. The positioning performance of triple-constellation static PPP was greater than that of GPS-only, GLONASS-only, and Galileoonly static PPP. Besides that, the performance was also better than that of the dual-system static PPP.

2. The convergence performance of triple-GNSS PPP was the best for all seven different static-PPP scenarios.

3. The number of satellites for the triple-constellation static PPP was significantly better than that of GPS-only PPP. GPS-only PPP had better satellite visibility than GLONASS and Galileo-only PPP.

4. The integration of GPS, GLONASS and Galileo static PPP solutions significantly lowers PDOP values.

This paper was limited to stations geographically distributed over Africa and incorporated Galileo other than BeiDou in the triple-GNSS static PPP solution. Thus, future research prospects will increase the number of stations and integrate BeiDou in the triple-GNSS static PPP solution.

References

Abd-Rabbou, M. and A. El-Rabbany. 2017. “Performance Analysis of Precise Point Positioning Using Multi-Constellation GNSS : GPS , GLONASS , Galileo and BeiDou.” 6265(May 2016).

Abd Rabbou, Mahmoud, Adel El-Shazly, and Kamal Ahmed. 2017. “Comparative Analysis of Multi-Constellation GNSS Single-Frequency Precise Point Positioning.” Survey Review, 1–10.

Afifi, Akram and Ahmed El-Rabbany. 2016. “Precise Point Positioning Using Triple GNSS Constellations in Various Modes.” Sensors (Switzerland) 16(6).

Altamimi, Zuheir and Richard Gross. 2017. “Geodesy.” Pp. 1039– 61 in Springer Handbook of Global Navigation Satellite Systems.

Azami, Hamed, Milad Azarbad, and Saeid Sanei. 2013. “New Applied Methods for Optimum GPS Satellite Selection.” in 2013 3rd Joint Conference of AI and Robotics and 5th RoboCup Iran Open International Symposium: Learning, Glorious Future, RIOS 2013.

Bisnath, S. and Y. Gao. 2009. “Current State of Precise Point Positioning and Future Prospects and Limitations.” in International Association of Geodesy Symposia. Cai, Changsheng and Yang Gao. 2013.

“Modeling and Assessment of Combined GPS/GLONASS Precise Point Positioning.” GPS Solutions 17(2):223–36.

Ceylan, Ayhan, Cemal Ozer YIGIT, Salih ALCAY, and Behlul Numan OZDEMIR. 2015. “EVALUATING THE PERFORMANCE OF KINEMATIC PPP AND DIFFERENTIAL KINEMATIC METHODS IN RURAL AND URBAN AREAS.” Pp. 17–21 in From the Wisdom of the Ages to the Challenges of the Modern World.

Choy, Suelynn, Sunil Bisnath, and Chris Rizos. 2017. “Uncovering Common Misconceptions in GNSS Precise Point Positioning and Its Future Prospect.” GPS Solutions 21(1):13–22.

Choy, Suelynn, Shaocheng Zhang, François Lahaye, and Pierre Héroux. 2013. “A Comparison between GPSOnly and Combined GPS+GLONASS Precise Point Positioning.” Journal of Spatial Science 58(2):169–90.

Gao, Yang and Kongzhe Chen. 2004. “Performance Analysis of Precise Point Positioning Using Rea-Time Orbit and Clock Products.” Journal of Global Positioning Systems.

Ge, M., G. Gendt, M. Rothacher, C. Shi, and J. Liu. 2008. “Resolution of GPS Carrier-Phase Ambiguities in Precise Point Positioning (PPP) with Daily Observations.” Journal of Geodesy.

Ge, Maorong, Hongping Zhang, Xiaolin Jia, Shuli Song, and Jens Wickert. 2012. “What Is Achievable with the Current Compass Constellation?” GPS World 23(11):29–33.

Geng, Jianghui et al. 2009. “Ambiguity Resolution in Precise Point Positioning with Hourly Data.” GPS Solutions 13(4):263–70.

Guo, Fei, Xingxing Li, Xiaohong Zhang, and Jinling Wang. 2017a. “Assessment of Precise Orbit and Clock Products for Galileo, BeiDou, and QZSS from IGS Multi-GNSS Experiment (MGEX).” GPS Solutions 21(1):279–90. Guo, Fei, Xingxing Li, Xiaohong Zhang, and Jinling Wang. 2017b. “The Contribution of Multi-GNSS Experiment (MGEX) to Precise Point Positioning.” Advances in Space Research 59(11):2714–25.

Guo, Jing, Xiaolong Xu, Qile Zhao, and Jingnan Liu. 2016. “Precise Orbit Determination for Quad-Constellation Satellites at Wuhan University: Strategy, Result Validation, and Comparison.” Journal of Geodesy.

Héroux, P. et al. 2004. “Products and Applications for Precise Point Positioning – Moving Towards Real-Time.” Proceedings of the 17th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2004).

Kaplan, E.D. 2006 Understanding GPS: Principles and Applications, Second Edition, 2nd edition, Boston: Artech House.

Kouba, Jan and Pierre Héroux. 2001. “Precise Point Positioning Using IGS Orbit and Clock Products.” GPS Solutions.

Leick, Alfred, Lev Rapoport, and Dmitry Tatarnikov. 2015. GPS Satellite Surveying: Fourth Edition.

Li, Xingxing et al. 2015. “Accuracy and Reliability of Multi-GNSS Real- Time Precise Positioning: GPS, GLONASS, BeiDou, and Galileo.” Journal of Geodesy 89(6):607–35.

Li, Xingxing, Xiaohong Zhang, and Fei Guo. 2009. “Study on Precise Point Positioning Based on Combined GPS and GLONASS.” Wuhan Daxue Xuebao Xinxi Kexue Ban Geomatics And Information Science Of Wuhan University 3(1):2449–59.

Lou, Yidong et al. 2016. “Multi- GNSS Precise Point Positioning with Raw Single-Frequency and Dual- Frequency Measurement Models.” GPS Solutions 20(4):849–62.

Loyer, Sylvain, Félix Perosanz, Flavien Mercier, Hugues Capdeville, and Jean Charles Marty. 2012. “Zero-Difference GPS Ambiguity Resolution at CNESCLS IGS Analysis Center.” Journal of Geodesy 86(11):991–1003.

Melgard, T., E. Vigen, K. de Jong, and O. Oerpen. 2009. “G2 – The First Real- Time GPS and GLONASS Precise Orbit and Clock Service.” in Proceedings of the 22nd International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2009).

Montenbruck, O., A. Hauschild, and P. Steigenberger. 2014. “Differential Code Bias Estimation Using Multi- GNSS Observations and Global Ionosphere Maps.” Navigation, Journal of the Institute of Navigation.

Odolinski, Robert, Peter J. G. Teunissen, and Dennis Odijk. 2014. “Combined BDS, Galileo, QZSS and GPS Single-Frequency RTK.” GPS Solutions 19(1):151–63.

Pan, L. et al. 2017. “Satellite Availability and Point Positioning Accuracy Evaluation on a Global Scale for Integration of GPS, GLONASS, BeiDou and Galileo.” Advances in Space Research.

Pan, Zongpeng, Hongzhou Chai, and Yulong Kong. 2017. “Integrating Multi- GNSS to Improve the Performance of Precise Point Positioning.” Advances in Space Research 60(12):2596–2606.

Rabbou, Mahmoud Abd and Ahmed El- Rabbany. 2015. “Precise Point Positioning Using Multi-Constellation GNSS Observations for Kinematic Applications.” Journal of Applied Geodesy 9(1):15–25.

Rizos, Chris et al. 2013. “The IGS MGEX Experiment as a Milestone for a Comprehensive Multi-GNSS Service.” in Proceedings of the Ion Pacific Pnt Meeting.

Schaer, S. 2017. “Bias and Calibration Working Group Technical Report 2017.” 2017:154–60.

Schönemann, Erik, Matthias Becker, and Tim Springer. 2011. “A New Approach for GNSS Analysis in a Multi- GNSS and Multi-Signal Environment.” Journal of Geodetic Science.

Shen, X. and Y. Gao. 2006. “Analyzing the Impacts of Galileo and Modernized GPS on Precise Point Positioning.” in Proceedings of the 2006 National Technical Meeting of The Institute of Navigation.

Soycan, Metin. 2012. “A Quality Evaluation of Precise Point Positioning within the Bernese GPS Software Version 5.0.” Arabian Journal for Science and Engineering 37(1):147–62.

Soycan, Metin and Ercenk Ata. 2011. “Precise Point Positioning versus Traditional Solution for GNSS Networks.” Scientific Research and Essays 6(4):799–808.

Steigenberger, P., A. Hauschild, O. Montenbruck, C. Rodriguez-Solano, and U. Hugentobler. 2013. “Orbit and Clock Determination of QZS-1 Based on the CONGO Network.” Navigation, Journal of the Institute of Navigation.

Tegedor, Javier et al. 2016. “Estimation of Galileo Uncalibrated Hardware Delays for Ambiguity-Fixed Precise Point Positioning.” Navigation, Journal of the Institute of Navigation.

Teunissen, Peter J. G. and Oliver Montenbruck. 2017. Springer Handbook of Global Navigation Satellite Systems.

Tolman, B.W., Kerkhoff, A., Rainwater, D., Munton, D., Bank, J. 2010 Absolute Precise Kinematic Positioning with GPS and GLONASS, Proceedings of the 23rd International Technical Meeting of The Satellite Division of the Institute of Navigation, Portland, OR, pp. 2565-2576.

Xia, Fengyu et al. 2018. “ScienceDirect Assessing the Latest Performance of Galileo-Only PPP and the Contribution of Galileo to Multi-GNSS PPP.” Advances in Space Research.

Yu, Xidong and Jingxiang Gao. 2017a. “Kinematic Precise Point Positioning Using Multi-Constellation Global Navigation Satellite System ( GNSS ) Observations.”

Yu, Xidong and Jingxiang Gao. 2017b. “Kinematic Precise Point Positioning Using Multi-Constellation Global Navigation Satellite System (GNSS) Observations.” ISPRS International Journal of Geo-Information. Zhang, Xu, Bin Xian, Bo Zhao, and Yao Zhang. 2015. “Autonomous Flight Control of a Nano Quadrotor Helicopter in a GPS-Denied Environment Using On-Board Vision.” IEEE Transactions on Industrial Electronics 62(10):6392–6403.

Zhao, X., S. Wang, C. Liu, J. Ou, and X. Yu. 2017. “Assessing the Performance of Multi-GNSS Precise Point Positioning in Asia-Pacific Region.” Survey Review 49(354):186–96.

Zhou, Feng et al. 2018. “GAMP: An Open-Source Software of Multi- GNSS Precise Point Positioning Using Undifferenced and Uncombined Observations.” GPS Solutions 22(2).

Zumberge, J. F., M. B. Heflin, D. C. Jefferson, M. M. Watkins, and F. H. Webb. 1997. “Precise Point Positioning for the Efficient and Robust Analysis of GPS Data from Large Networks.” Journal of Geophysical Research: Solid Earth 102(B3):5005–17.