Spatially Smart Wine

Fadhillah Norzahari New South Wales Young Surveyors

Kate Fairlie New South Wales Young Surveyors

Adrian White New South Wales Young Surveyors

Mitchell Leach New South Wales Young Surveyors

Mark Whitty School of Mechanical and Manufacturing Engineering, University of New South Wales, Australia

Stephen Cossell School of Mechanical and Manufacturing Engineering, University of New South Wales, Australia

Jose Guivant School of Mechanical and Manufacturing Engineering, University of New South Wales, Australia

Jayantha Katupitiya School of Mechanical and Manufacturing Engineering, University of New South Wales, Australia

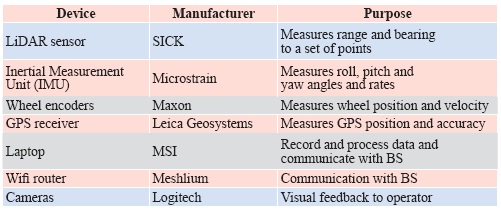
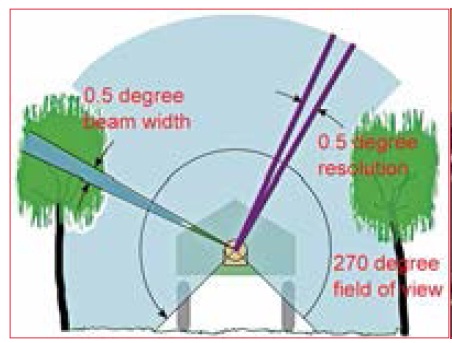
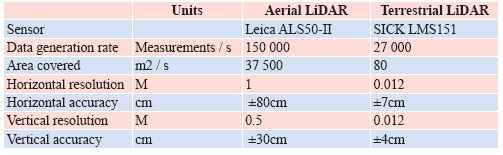
Unmanned Ground Vehicle (UGV): Testing and applications

Here we present an Unmanned Ground Vehicle (UGV) which contains technologies for automated yield estimation which are readily applicable to many existing agricultural machines. The UGV was developed in the School of Mechanical and Manufacturing Engineering at the University of New South Wales under the direction of Associate Professor Jayantha Katupitiya and Dr Jose Guivant. As shown in Figure 4, it is a four wheeled vehicle equipped with sensors and actuators for teleoperation and full autonomous control. Weighing 50kg, it is a comprised of Commercial-Off-the-Shelf (COTS) sensors, a custom-made mechanical base and a low-cost onboard laptop with a wireless connection to a remote Base Station (BS). Of particular note is ready retrofi tting capacity of the COTS sensors to existing farm machinery.
For the purposes of this paper, the vehicle was tele-operated from the nearby BS with the operator manoeuvring with the aid of three onboard video cameras and a display of the LiDAR data in realtime. Autonomous operation using the LiDAR data and was demonstrated in Whitty et al. (2010)(For videos, see our YouTube channel: www. youtube.com/UNSWMechatronics).

System overview

The equipment contained in the vehicle is shown in Table 4. Of this the relevant items are the rear 2D LiDAR sensor, the IMU, the CORS-corrected GPS receiver and the wheel encoders. Together with the onboard computer, these items allow accurate georeferenced point clouds to be generated which are accurate to 8cm. The output is not limited to point clouds, as any other appropriately sized sensors can be integrated to provide precise positioning of the sensed data, either in real-time or by post-processing.

Measurement estimation and accuracy

The following paragraphs show how the pose of the robot is accurately estimated and then how this pose is fused with the laser data to obtain 3D point clouds. Given the uncertainty of the robot pose, we also derive expressions for the resultant uncertainty of each point in the point cloud. Furthermore, the average case accuracy is compared with that obtained from aerial LiDAR and the advantages and disadvantages of both methods of data gathering are discussed from the perspective of PV.

Figure 4: UGV with relevant equipment labelled

Table 4: UGV Equipment

As discussed, the CORS-linked GPS sensor mounted o n the UGV provides both the position and position uncertainty of the vehicle in ECEF coordinates. In this case the MGA55 frame was used to combine all the sensor data for display in one visualisation package. The GPS position was provided at 1Hz and given the high frequency dynamics of the robot’s motion, higher frequency position estimation was necessary. Hence an inertial measurement unit (IMU), containing accelerometers and gyroscopes, was mounted on the vehicle providing measurements at 200Hz. The output of this IMU was fused with the wheel velocities as described in (Whitty et al., 2010) to estimate the short term pose of the vehicle between GPS measurements. The IMU also provided pitch and roll angles, which were used in combination with the known physical offset of the GPS receiver to transform the GPS provided position to the coordinate system of the robot.

Given the time of each GPS measurement (synchronised with the IMU readings), the set of IMU derived poses between each pair of consecutive GPS measurements was extracted. Assuming the heading of the robot had been calculated from the IMU readings, the IMU derived poses were projected both forwards and backwards relatively from each GPS point. The position of the robot was then linearly interpolated between each pair of these poses, giving an accurate and smooth set of pose estimates at a rate of 200Hz. Since the GPS measurements were specifi ed in MGA55 coordinates and the pose estimates calculated from these, the pose estimates were therefore also found in MGA55 coordinates.

The primary sensor used for mapping unknown environments was the SICK LMS151 2D laser rangefi nder. Figure 6 pictures one of these lasers, which provided range readings up to a maximum of 50m with a 1σ statistical error of 1.2cm. Figure 5 shows the Field of View (FoV) as 270° with the 541 readings in each scan spaced at 0.5° intervals and recorded at a rate of 50Hz, giving about 27 000 points per second. Its position on the rear of the robot was selected to give

Figure 5: 2D Field of View (FoV), showing scan of vines

Figure 6: LiDAR sensor on the UGV

the best coverage of the vines on both sides as the robot moves along a row. To accurately calculate the position of each scanned point, we needed to accurately determine the position and orientation of the laser at the time the range measurement was taken. All of the IMU data and laser measurements were accurately time stamped using Windows High Performance Counter so the exact pose could be interpolated for the known scan time. Given the known offset of the laser on the vehicle, simple geometrical transformations were then applied to project the points from range measurements into space in MGA55 coordinates. Complete details are available in Whitty et al., (2010) which was based on similar work in Katz et al. (2005) and Guivant (2008). This calculation was done in real-time, enabling the projected points – collectively termed a point cloud – to be displayed to the operator as the UGV moved.

Information representation to operator

The display of the point cloud was done using a custom built visualisation program which was also adapted to read in a LiDAR point cloud and georeferenced aerial imagery obtained from a fl ight over the vineyard. Since all these data sources were provided in MGA55 coordinates, it was a simple matter to overlay them to gain an estimate of the accuracy of the laser measurements. Figure 7 shows the terrestrial point cloud overlaid on the image data where the correspondence is clearly visible. Given that the pointcloud is obtained in 3D, this provides the operator with a full picture of the vineyard which can be viewed from any angle.

Table 5: Comparison of aerial and terrestrial LiDAR systems (values are approximate)

Fusion of sensor data and calculation of accuracy

Although the above point cloud generation process has been described in a deterministic manner, in practice measurement of many of the robot parameters is usually not precise. By performing experiments, we were able to characterise these uncertainties individually and then combine them to estimate the uncertainty in position of every point we measured. In the fi eld of robotics, these uncertainties are typically characterised as a covariance matrix based on the standard deviations of each quantity, assuming that they are normally distributed. The covariance matrix giving the uncertainty of the UGV’s pose in MGA55 coordinates is a 6×6 matrix. The UGV’s pose itself is given by a vector which concatenates the 3D position and the orientation given in Euler angles.

Since the GPS receiver was offset from the origin of the UGV’s coordinate system, the GPS provided position was transformed to the UGV’s coordinate system by rigid body transformation. However, the uncertainty of the angular elements of the pose meant that the GPS uncertainty must not only be shifted but be rotated and skewed to refl ect this additional uncertainty. An analogy is that of drawing a straight line of fi xed length with a ruler. If you don’t know exactly where to start, then you have at least the same uncertainty in the endpoint of the line. But if you also aren’t sure about the angle of the line, the uncertainty of the endpoint is increased.

A similar transformation of the UGV uncertainty to the position of the laser scanner on the rear of the UGV provided the uncertainty of the laser scanner’s position. Then for every laser beam projected from the laser scanner itself, a further transformation gave the covariance of the projected point due to the angular uncertainty of the UGV’s pose.

Additionally, we needed to take into account uncertainty in the measurement angle and range of individual laser beams. This followed a similar pattern and the uncertainty of the beam was calculated based on a standard deviation of 0.5 degrees in both directions due to spreading of the beam. Once the uncertainty in the beam, which was calculated relative to the individual beam, was found, it was rotated fi rst to the laser coordinate frame and then to the world coordinate frame using the corresponding rotation matrices. Finally, the uncertainty of the laser position was added to give the uncertainty of the scanned point.

Figure 7: UGV generated point-cloud with overlay of aerial imagery

Comparison of aerial and terrestrial LiDAR

An experiment was conducted at the location detailed in Section 1.2. The UGV was driven between the rows of vines to measure them in 3D at a speed of about 1m/s. The average uncertainty of all the points was calculated and found to be 8cm in 3D. Table 5 shows how this compares with about 1.2m for the aerial LiDAR but has the disadvantage of a much slower area coverage rate. The major advantages however are the increased density of points (~3000 / m3), ability to scan the underside of the vines and greatly improved resolution. Also, the terrestrial LiDAR can be retrofi tted to many existing agricultural vehicles and used on a very wide range of crops. Limited vertical accuracy – a drawback of GPS – is a major restriction but this can be improved by calibrating the system at a set point with known altitude.

For PV, the terrestrial LiDAR system clearly offers a comprehensive package for precisely locating items of interest. Further developments in processing the point clouds will lead to estimation of yield throughout a block and thereby facilitating implementation of performance adjusting measures to standardise the yield and achieve higher returns. For example, a mulch delivery machine could have its outfl ow rate adjusted according to its GPS position, allowing the driver to concentrate on driving instead of controlling the mulch delivery rate. This not only reduces the amount of excess mulch used but reduces the operator’s workload, with less likelihood of error such as collision with the vines due to fatigue.

Conclusion

In this paper we have evaluated several state-of-the-art geospatial technologies for precision viticulture including multilayered information systems, GNSS receivers, Continuously Operating Reference Stations (CORS) and related hardware. These technologies were demonstrated to support sustainable farming practices including organic and biodynamic principles but require further work before their use can be widely adopted. Limitations of the current systems were identifi ed in easeof- use and more particularly in the lack of a unifi ed data management system which combines fi eld and offi ce use. While individual technologies such as GIS, GNSS and handheld computers exist, their integration with existing geospatial information requires the expertise of geospatial professionals, and closer collaboration with end users.

In addition we demonstrated the application of an unmanned ground vehicle which produced centimetrelevel feature position estimation through a combination of terrestrial LiDAR mapping and GNSS localisation. We compared the accuracy of this mapping approach with aerial LiDAR imagery of the vineyard and showed that apart from coverage rate the terrestrial approach was more suited in precision viticulture applications. Future work will focus in integrating this approach with precision viticulture machinery for estimating yield and controlling yield-dependent variables such as variable mulching, irrigation, spraying and harvesting. The end product? Spatially smart wine.

Acknowledgements

The authors wish to acknowledge the following bodies and individuals who provided equipment and support: Land and Property Management Authority (in particular Glenn Jones), CR Kennedy (in particular Nicole Fourez), ESRI Australia and the University of New South Wales. Particular thanks go to the vineyard owner and manager, Justin Jarrett and family.

References

Arnó, J., Martínez-Casasnovas, J., Ribes-Dasi, M. & Rosell, J. (2009) Review. Precision Viticulture. Research topics, challenges and opportunities in site-specifi c vineyard management. Spanish Journal of Agricultural Research, 7, 779-790.
Battaglini, A., Barbeau, G., Bindi, M. & Badeck, F. W. (2009) European winegrowers’ perceptions of climate change impact and options for adaptation. Regional Environmental Change, 9, 61-73.
Bramley, R. (2009) Lessons from nearly 20 years of Precision Agriculture research, development, and adoption as a guide to its appropriate application. Crop and Pasture Science, 60, 197-217.
Bramley, R., Proffi tt, A., Hinze, C., Pearse, B., Hamilton, R. & Stafford, J. (2005) Generating benefi ts from precision viticulture through selective harvesting. Wageningen Academic Publishers.
Bramley, R. & Robert, P. (2003) Precision viticulture-tools to optimise winegrape production in a diffi cult landscape. American Society of Agronomy.
Chaoui, H. I. & Sørensen, C. G. (2008) Review of Technological Advances and Technological Needs in Ecological Agriculture (Organic Farming).
Dedousis, A. P., Bartzanas, T., Fountas, S., Gemtos, T. A. & Blackmore, S. (2010 ) Robotics and Sustainability in Soil Engineering. Soil Engineering. Springer Berlin Heidelberg.
Delmas, M. A. & Grant, L. E. (2008) Eco-labeling strategies: the ecopremium puzzle in the wine industry.
Fairlie, K. & Mcalister, C. (2011) Spatially Smart Wine – Getting Young Surveyors to Network in the Vineyard! And other Australian young surveyor activities. . International Federation of Surveyors Working Week 2011. Marrakech, Morocco.
Gebbers, R. & Adamchuk, V. I. (2010) Precision Agriculture and Food Security. Science, 327, 828-831.
GIL, E. (2007) Variable rate application of plant protection products in vineyard using ultrasonic sensors. Crop Protection, 26, 1287-1297.
Grift, T., Zhang, Q., Kondo, N. & Ting, K. (2008) A review of automation and robotics for the bioindustry. Journal of Biomechatronics Engineering, 1, 37-54.
Grote, K., Hubbard, S. & Rubin, Y. (2003) Field-scale estimation of volumetric water content using groundpenetrating radar ground wave techniques. Water Resour. Res, 39, 1321.
Guivant, J. E. (2008) Real Time Synthesis of 3D Images Based on Low Cost Laser Scanner on a Moving Vehicle. V Jornadas Argentinas de Robotica, Bahia Blanca.
Hall, A., Louis, J. & Lamb, D. (2003) Characterising and mapping vineyard canopy using high-spatial-resolution aerial multispectral images. Computers & Geosciences, 29, 813-822.
Johnson, L., Roczen, D., Youkhana, S., Nemani, R. & Bosch, D. (2003) Mapping vineyard leaf area with multispectral satellite imagery. Computers and Electronics in Agriculture, 38, 33-44
. Katz, R., Melkumyan, N., Guivant, J., Bailey, T. & Nebot, E. (2005) 3D sensing framework for outdoor navigation. Australian Conference on Robotics and Automation (ACRA), Proceedings of. Citeseer.
Keightley, K. E. & Bawden, G. W. (2010) 3D volumetric modeling of grapevine biomass using Tripod LiDAR. Computers and Electronics in Agriculture, 74, 305-312.
Kirchmann, H. (1994) Biological dynamic farming—An occult form of alternative agriculture? Journal of Agricultural and Environmental Ethics, 7, 173-187.
Lamb, D., Bramley, R. & Hall, A. (2002) Precision viticulture-an Australian perspective. ISHS.
Leica Geosystems (2009) Leica Zeno 10 & Zeno 15.
Longo, D., Pennisi, A., Bonsignore, R., Muscato, G. & Schillaci, G. (2010) A Multifunctional Tracked Vehicle Able to Operate in Vineyards Using GPS and Laser Range-fi nder Technology. International Conference Ragusa SHWA2010 – September 16- 18 2010 Ragusa Ibla Campus – Italy “Work safety and risk prevention in agro-food and forest systems”.
López Riquelme, J., Soto, F., Suardíaz, J., Sánchez, P., Iborra, A. & Vera, J. (2009) Wireless sensor networks for precision horticulture in Southern Spain. Computers and Electronics in Agriculture, 68, 25-35.
Matese, A., Di Gennaro, S., Zaldei, A., Genesio, L. & Vaccari, F. (2009) A wireless sensor network for precision viticulture: The NAV system. Computers and Electronics in Agriculture, 69, 51-58.
Mazzetto, F., Calcante, A., Mena, A. & Vercesi, A. (2010) Integration of optical and analogue sensors for monitoring canopy health and vigour in precision viticulture. Precision Agriculture, 1-14.
Mcbratney, A., Whelan, B., Ancev, T. & Bouma, J. (2005) Future directions of precision agriculture. Precision Agriculture, 6, 7-23.
Morais, R., Fernandes, M. A., Matos, S. G., Ser Dio, C., Ferreira, P. & Reis, M. (2008) A ZigBee multipowered wireless acquisition device for remote sensing applications in precision viticulture. Computers and Electronics in Agriculture, 62, 94-106.
Proffi tt, T. (2006) Precision viticulture: a new era in vineyard management and wine production, Winetitles.
Reeve, J. R., Carpenter-Boggs, L., Reganold, J. P., York, A. L., Mcgourty, G. & Mccloskey, L. P. (2005) Soil and winegrape quality in biodynamically and organically managed vineyards. American journal of enology and viticulture, 56, 367.
Rosell, J. R., Llorens, J., Sanz, R., Arnó, J., Ribes-Dasi, M. & Masip, J. (2009) Obtaining the three-dimensional structure of tree orchards from remote 2D terrestrial LIDAR scanning. Agricultural and Forest Meteorology, 149, 1505-1515.
Rosell Polo, J. R., Sanz, R., Llorens, J., Arnó, J., Escol , A., Ribes-Dasi, M., Masip, J., Camp, F., Gr Cia, F. & Solanelles, F. (2009) A tractor-mounted scanning LIDAR for the non-destructive measurement of vegetative volume and surface area of tree-row plantations: A comparison with conventional destructive measurements. Biosystems Engineering, 102, 128-134.
Rowbottom, B., Hill, M., Valley, Y., Heathcote, B. & Strathbogie, B. (2008) Managing the nutrition of grapevines. Australian viticulture, 12, 85.
Shanmuganthan, S., Ghobakhlou, A. & Sallis, P. (2008) Sensor data acquisition for climate change modelling. WSEAS Transactions on Circuits and Systems, 7, 942-952.
Shi, L., Miao, Q. & Jinglin, D. (2008) Architecture of Wireless Sensor Networks for Environmental Monitoring. Education Technology and Training, 2008. and 2008 International Workshop on Geoscience and Remote Sensing. ETT and GRS 2008. International Workshop on.
Siegfried, W., Viret, O., Huber, B. & Wohlhauser, R. (2007) Dosage of plant protection products adapted to leaf area index in viticulture. Crop Protection, 26, 73-82.
Turinek, M., Grobelnik-Mlakar, S., Bavec, M. & Bavec, F. (2009) Biodynamic agriculture research progress and priorities. Renewable Agriculture and Food Systems, 24, 146-154.
Whitty, M., Cossell, S., Dang, K. S., Guivant, J. & Katupitiya, J. (2010) Autonomous Navigation using a Real- Time 3D Point Cloud. 2010 Australasian Conference on Robotics and Automation. 1-3 December 2010 Brisbane, Australia.