GPS surveyed time-invariant sea floor depths for safe navigation

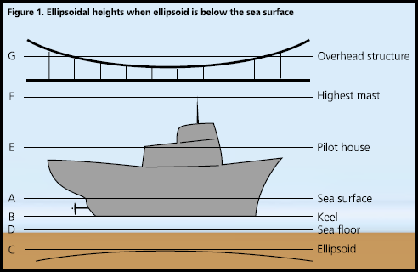
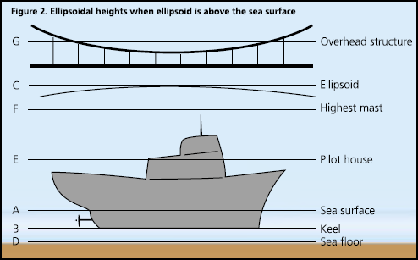
For safe sailing, two most important requirements are to be able to determine clearances between the sea floor and the keel of the ship, and between the mainmast and overhead structures, such as cables and bridges. For these clearances, the mariner has to know correctly and accurately the following:1. Location of the sea floor or ocean depth,2. Height of the overhead structure,3. Locations of the ship’s keel and mainmast.

For centuries and even in the present practice, the above four surveyed positions are referenced to more than one datum. Further more, these datums are time-dependent and time-variant.

We propose that the two clearances or the four positions are measured with respect to one time-invariant ellipsoidal surface as zero reference. Then, the mariners would have PHDthem correctly and accurately in one datum, whenever required. In shallow waters and inside harbors, the captain of a ship would be able to measure the clearances accurately and with confidence to avoid grounding or striking overhead obstructions, such as bridges and cables.

Combining GPS surveys and acoustic soundings, highly accurate ellipsoidal depths of the sea floor can be established in new areas or by filling gaps independent of the stage of the tide and any tidal datum. In separate GPS surveys, the ellipsoidal heights for overhead structures can be determined. The time-invariant sea floor depths and heights of the overhead structures can then be stored in the Marine Information System (MIS) database for future use. While underway in shallow waters, in berthing, in approaching channels, and inside harbor, using a mainmast-mounted GPS antenna and the ship’s general arrangement drawings, the shipboard computer will determine the

positions of the ship’s keel, mainmast, and Plimsoll marks. Then, recovering the already established sea floor depths and overhead heights, it can compute the two clearances for safe navigation without any reference to the time-variant tides, tidal datum(s), and ship’s draft.

This article describes the surveying mode to establish time-invariant ellipsoidal depths or heights of the sea floor in the open ocean. A few additional survey procedures have been specified to achieve higher accuracy for shallow waters and inside harbors. A step by step algorithm is also included to compute the ship’s two vertical clearances.

Surveying the sea floor and overhead structures

In the marine scenario, the Ellipsoid of the World Geodetic System (WGS) 1984, the coordinate system used within GPS, is both below and above the sea surface, which can result in the surveyed ellipsoidal depths or heights to be plus or minus respectively. In the following figures, ellipsoidal depths or heights are positive upwards with respect to the ellipsoidal surface.

A. When the WGS 84 Ellipsoid is below the sea surface – Figure 1 shows schematic locations for the overhead structure, ship’s mainmast, pilothouse deck, and keel, sea surface, sea floor, and ellipsoidal zero reference surface.
DC = Ellipsoidal Height
of sea floor (+h)

AC = Ellipsoidal Height
of sea surface (+h)

BC = Ellipsoid Height
of ship’s Keel (+h)

CE = Ellipsoidal Height
of the Pilothouse (+h)

CF = Ellipsoid Height
of Ship’s Mainmast (+h)

CG = Ellipsoid Height
of the Overhead Structure (+h)

BD = Depth of Sea Floor from keel as measured by acoustic sounding.

During the GPS surveying, the distance BD between the ship’s keel and sea floor will be measured with presently used acoustic sounding techniques. Then, the ellipsoid height (h) of the sea floor DC will be

DC = BC – BD = [CF – BF] – BD

In this configuration, the distances CF, BF, and BD are measured during GPS surveys without any reference to the stage of the tide and/or tidal surface. This is the decided advantage over the depths determined with respect to time-variant tidal datums.

In many cases, especially in deep water, the sea floor will be below the ellipsoid and have a negative height (-h). Here, the accuracy of the distance BD is accepted as achievable by acoustic techniques.

B. When the WGS 84 Ellipsoid is above the sea surface – Figure 2 shows schematic locations when the ellipsoid is above the sea surface.

DC = Ellipsoidal Height
of sea floor (- h)

AC = Ellipsoidal Height
of sea surface (-h)

BC = Ellipsoid Height
of ship’s Keel (-h)

CE = Ellipsoidal Height
of the Pilothouse (-h)

CF = Ellipsoid Height
of Ship’s Mainmast (-h)

CG = Ellipsoid Height
of Overhead Structure (+h)

BD = Depth of Sea
Floor from keel as measured by acoustic sounding.

In this case, the ellipsoid depth

of sea floor DC will be

DC = – BC – BD = – [CF + BF] – BD.

It may be pointed out that near Sri Lanka, the ellipsoid height of the sea surface AC has a maximum “low” of about -100 meters and this particular type of geometry is mostly not known to many users, particularly mariners.