| Geodesy - New | |
On the transformation of time system in relativity based on SOFA and .NET
According to assembly of the transformation of time system in relativity provided by Standards Of
|
 |
|
 |
|
 |
|
Time originally determined by the standard clock is called proper time, and the time calculated under the relativistic framework is called coordinate time. The time conversion calculated under the relativistic framework comes to precession, nutation, and polar motion correction models which calculate complexly and are more difficult to write a program, so the IAU gives ‘Standards of Fundamental Astronomy’ (SOFA) to achieve the computational model. Currently, SOFA has two versions of FORTRAN and C. FORTRAN, as an old programming language by virtue of its powerful computing capability, is still used in some scientific computing and engineering projects. However, FORTRAN runs under DOS unfriendly interface that makes its operation less convenient. C# language that has recently emerged under .NET platform makes up for the lack of FORTRAN. With the rapid development of its technology and user-friendly interface, C# has been widely used in the windows platform.
In this paper, the advantages of FORTRAN’s efficient algorithms and C#’s friendly interface are combined. The mixed programming based on FORTRAN and C# is researched, and relativistic frame time conversion system has been studied by analyzing the SOFA assemblies.
Time system in relativity
Terrestrial Time (TT)
Temps Dynamigue Terrestre (TDT), based on the International Atomic Time (TAI), is geocentric coordinate time, whose second length is the same as TAI. The relationship between them is [1]:
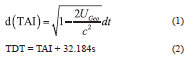
In the 21st IAU meeting, Temps Dynamigue Terrestre (TDT) was formally changed to Terrestrial Time (TT). According to the relationship between proper time τ and TT, after ignoring items O(c-4), the relationship between the two under post-Newtonian accuracy is [2] :
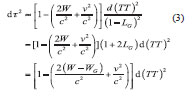
where W is contained gravitational potential and perturbation celestial TGP measuring sites’ phase function in the Earth center of mass reference frame; v is the observer dimensional velocity in the non-rotating earth’s center of mass reference frame; and WG is geoid gravity position.
Temps Coordinate Geocentrigue (TCG)
Temps Coordinate Geocentrigue is the time basis of Geocentric Celestial Reference System (GCRS) that is set by IAU. Its function is to switch TDT from geoid to center of the earth under the relativistic framework, and the relationship between the two is:
![]()
![]()
where LG is similar to formula (4).
Temps Coordinate Barycentrigue (TCB) Temps Coordinate Barycentrigue is the time basis of Barycentric Celestial Reference System (BCRS). It is suitable for assumption that the observation station is still in the solar system (especially on the sun) and regardless of other factors. The calculation of TCB includes the time variable of planetary movement around the sun and the preparation of the planetary ephemeris time.
Temps Dynamigue
Barycentrigue (TDB) The result of the equations of motion of major planets comes from numerical integration of its argument just coordinate time, so people look at the TDB as coordinate time whose precise definition depends on the solar system CMCS coordinates and choice of metric. Its role is solving planetary motion around the sun and the preparation time motion equation system ephemeris used.
Mixed programming of SOFA and .NET
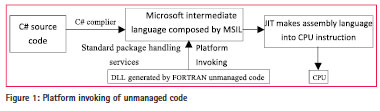
Development environment and principle introduction
The development environment of mixed programming is Visual Studio 2013; Intel Visual FORTRAN 2013 is embedded in .NET platform. Generally, t he executable code under control of the Common Language Runtime (CLR) is called the managed code. The code outside the runtime library is called unmanaged code. FORTRAN program in VS (Visual Studio) platform is unmanaged code, so the standard package handling services are used to generate dynamic link library DLL. Unmanaged code calling schematic is shown in Figure 1.
Realization of mixed programming
Firstly, a Dynamic-link Library (DLL) is created in IVF (Intel Visual Fortran). In order to be called by C#, the relativistic framework on time functions in SOFA library is added to the project.
Modify description of FORTRAN routines.
As FORTRAN and C# are two different languages, there are some differences in grammar and sentence structure between them. To achieve the call of DLL of FORTRAN in .NET platform, some modifications must be done:
(1) FORTRAN language is not case sensitive. When the compiler extracts function from a DLL, the function name will automatically be converted to all uppercase, as the .NET platform can’t find functions of FORTRAN source code. The ALIAS (alias) property should be used in the routine which specifies the export function name. Here in the iau_CAL2JD function of SOFA library function as an example (the same below), a line of code is added in a statement after the implicit none:
![]()
(2) When a DLL is created, the DLLEXPORTS property must be used in FORTRAN code to add an export declaration, which is a necessary step of importing routine. A line of code after implicit none is added:
![]()
(3) C# arrays start at 0 and its execution order is row column. FORTRAN arrays start at 1 and its execution order is column row. When performing the array parameter passing, the first element of the array is passed through to achieve the purpose of passing the first address of the array.
(4) Data for the value type in C# is directly stored in the stack. FORTRAN defaults type is a reference type. The address of the reference parameters is stored on the stack. The numerical value is stored in the heap. When stating or calling a function in C#, the ref keyword is used to modify parameters and make it to be a reference type.
The .NET call instructions:
When SOFA library DLL has been generated, it should be copied to the project directory Debug, then FORTRAN DLL can be called in C# project program and some statements should be made in the program.
(1) First of all, references of dynamic link library operations class should be added in C# using System. Runtime.Interopserviers.
(2) .NET platform Dlllmport property is used for C# language to access all API of WIN32 platforms. Property of SetLastError and CharSet are set to true. By setting property of CallingConvention to Stdcall, unity between the two will be achieved.
(3) When a SOFA function is called under .NET platform, it must be declared that the function is achieved from outside program module. Here the extern keyword should be used to modify the method name. The method must be called in public and static form.
Time system conversion under the relativistic framework
The latest version of the SOFA library (as of October 2014) has a total of 186 subprograms. The subprograms at present comprise 131 ‘astronomy’ routines supported by 55 ‘vector/matrix’ routines, available in both Fortran77 and C implementations [4]. The ‘astronomy’ library comprises 131 routines. The areas addressed include calendars, time scales, ephemerides, precessionnutation, star space−motion, star catalog transformations and geodetic/geocentric transformations. The ‘vector−matrix’ library, comprising 55 routines, contains a collection of simple tools for manipulating the vectors, matrices and angles used by the astronomy routines. This paper uses the two parts functions of SOFA to achieve the time system conversion under the framework of the relativistic [5].
TT and TCG conversion
The relativistic effects into Equation (5) can be obtained [6]:
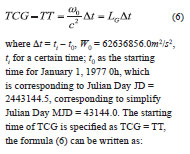
![]()
When SOFA library is used for time system conversion, the function iau_ DTF2D should be called to convert the time to SOFA internal format at first (the details of function, please refer to the literature [7], the same below). Then iau_UTCTAI function should be called to convert UTC to TAI. iau_TAITT function is called to convert TAI to TT. iau_ TTTCG function is called to convert TT to TCG. In this way, the conversion between TT and TCG has been indirectly achieved.
TT and TDB conversion
TDB is coordinate time. In literature [2], there is the following relationship between TDB and TT:
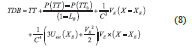
where the meaning of TT0 and t0 in formula (6) is identical. P (TT) is given by the ‘FBL’ analytical model, using numerical integration methods to calculate. Uext represents Newton potential of all solar system objects except earth (calculated at geocentric). VE, XE represent respectively geocentric orbital velocity vector and the position vector of the Barycentric Celestial Reference System (BCRS). X is the position vector of BCRS. TDB is indirectly calculated by calculating difference between the TDB and TT in SOFA function library. At first, function iau_DTDB is called to find difference between the two. It is the most complicated to calculate UT. UT = UT1-UT = + 0.3341 can be checked on the official line from the IERS. hen, iau_UTCUT1 function is called to convert UTC to UT1.
![]()
where MOD is the function that strives for the remainder of the FORTRAN language. And then, DTR = iau_DTDB function is called to calculate the difference between the TT and TDB, where U, V can be calculated in two ways: (1), by relations of converting geodetic coordinate system and the meridian plane Cartesian coordinates [8].
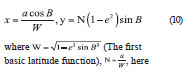
where (The first basic latitude function), , here the WGS-84 ellipsoid is taken and x, y represent respectively U and V. (2), by calling iau_GD2GC function to calculate the U, V.
![]()
Finally, function iau_TTTDB is called to calculate the TDB.
TT and TCB conversion
TT and TCB have no direct geometrical linear relationship, conversion of which can be achieved by the intermediate variable TDB. In previous section, a conversion relationship is given between TT and TDB. If the conversion relationship between TDB and TCB is given, TT and TCB conversion can be successfully achieved. There is the following relationship between TDB and TCB [9]:

TCB conversion can be achieved.
TCB and TCG conversion
According to movement rules under the major planets orbit perturbations of the earth centroid trajectory, and considering the geocentric orbital velocity and gravity of the sun and other planets as well as the full potential of GR dimensional transformation, the following conversion relationship exists between TCG and TCB:
![]()
where ti is a certain time of TCB, t0 is consistent with the January 1, 1977 TAI time. The meaning of Uext, Ve, Xe and X are the same as the one in formula (8). After ignoring items O(c–4), the relationship between the two under post-Newtonian accuracy is:
![]()
where the meaning of LC is as same as the one in formula (13), the meaning of VE, X as in formula (14) and M represent the mean anomaly.
In SOFA library, the conversion between TCB and TCG can also be conducted indirectly. In turn, calling iau_TCBTDB, iau_TDBTT and iau_TTTCG three functions, the indirect conversion between TCB and TCG can be achieved.
Examples of conversion
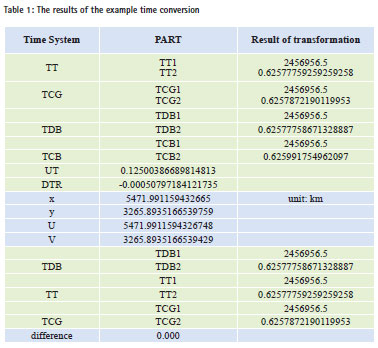
This example uses Wuhan October 26, 2014, 15:00 (UTC) as the initial data (the same below). The value of TT, TCG, TDB, and TCB are calculated and the self-consistency of time conversion is analyzed under the framework of the relativistic. According to the calculated results, subtraction is done and difference items will be got. The result is shown in Table 1.
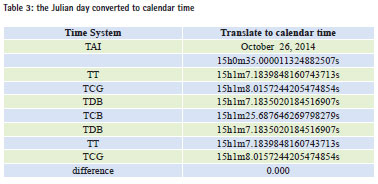
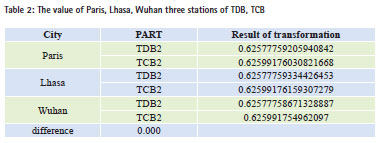
The order for time conversion is UTC- >TAI->TT->TCG, TT->TDB->TCB. And then TT, TCG, TDB, TCB can be obtained. In turn, the reverse calculation function is used to calculate TCB-> TDB- > TT-> TCG, and then TDB, TT, TCG will be got conversely. Table 2 shows the results of TT, TCG and TDB obtained by positive sequence, which is exactly the same as the reverse results obtained. So the differential item is 0 that indicates the self-consistency of the transitions between the various time systems as very good. When solving TDB, the difference of x and Y, or of U and V is small, which indicates that both methods can be applied. In seeking TCB and TDB time system conversion value, the calculation involves the longitude and latitude. Here we take three sites of Paris, Lhasa and Wuhan, and October 26, 2014, 15:00 (UTC) time as initial time; TDB and TCB are solved respectively. Because TT does not involve solving the latitude and longitude, here the fractional part of the day time that is only listed to avoid repetition.
In Table 2, TDB and TCB of three stations appear different, which is because longterm coefficient of the provisions of IAU and TDB in formula (8) has been removed, which is a direct result of TT. And TDB unit length is inconsistent. After solving TCB through TDB, it will make a difference. In order to make a more intuitive feel of the self-consistency about time conversion under relativistic framework, the calculated Julian date is converted to calendar time. The conversion results of which are shown in Table 3. It can be seen that the time conversion has a good self-consistency.
Conclusions
This paper systematically describes the conversion between the TT, TCB, TDB, TCB-time system under the framework of the theory of relativity, and gives & explains some of the functional relationship between them. Then, the implementation of principle of mixed programming is discussed, and so are the considerations in detail.
Finally, the mixed programming is used to solve examples. It can be seen that the result of the positive sequence call and reserve call of SOFA function library are identical. And the differential item is 0, which well illustrates the good self-consistency of time conversion under relativistic framework based on SOFA function library.
Acknowledgments
This research was funded by the national ‘863 Project’ of China (No. 2008AA12Z308) and National Natural Science Foundation of China (No. 41374012).
References
[1] Huang Tianyi, Xu Bangxin. Time Scales in Relativity [J]. PROGRESS IN ASTRONOMY, 1989, 7 (1):49-50.
[2] ZHANG Han-wei, MA Guoqiang, etc. The Definition and Application of Concorning Time in the Framework of Relativity [J]. Journal of Institute of Surveying and Mapping. 2004, 21 (3):161-162.
[3] ZHOU Zhen-hong, REN Hui, etc. Fortran DLL component being integrated into Microsoft .NET framework [J].Engineering Journal of Wuhan University. 2005, 38 (4):101-102.
[4] WEI Erhu, CHANG Liu, etc. Transformation Between ICRS and ITRS Based on SOFA [J]. Journal of Geomatics. 2012, 37 (1):31-32.
[5] Han Chunhao. Time Measurement Within the Framework of Relativity [J]. PROGRESS IN ASTRONOMY. 2002, 20 (2): 109-111.
[6] IERS Conventions(2003), D.D.McCautly & Petit(eds.), Frankfurt and Main, (2004)
[7] International Astronomical Union. SOFA TimeScaleandCalenderTools[EB/ OL].[2012-12-24].
[8] Kong Xiangyuan, Guo Jiming, Liu Zongquan .Foundation of Geodesy [M].WUHAN: WUHAN UNIVERSITY PRESS, 2010.
[9] IERS.IAUinformationbuller[EB/OL]. [20040801]. http://hpiers.Obspm.fr/eoppc/bul/bulb/explanatory.html.
[10] Zhenghang LI, Erhu WEI, et al. Space Geodesy [M], WUHAN: WUHAN UNIVERSITY PRESS, 2010.













 (8 votes, average: 4.38 out of 5)
(8 votes, average: 4.38 out of 5)




Leave your response!