Optimizing gravimetric geoid solution

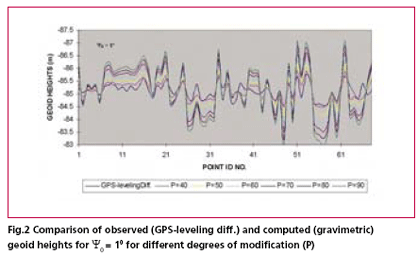
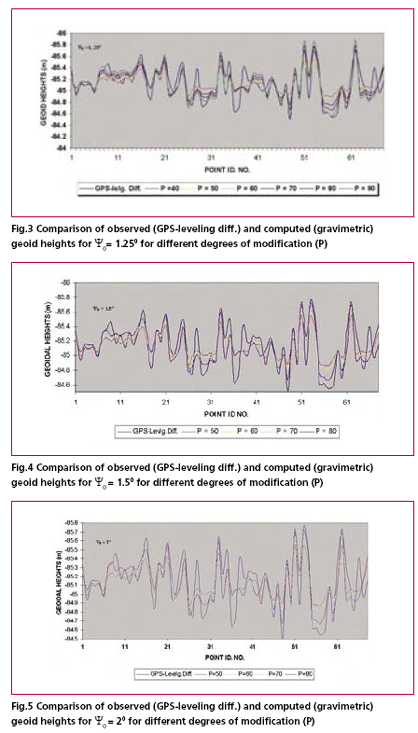
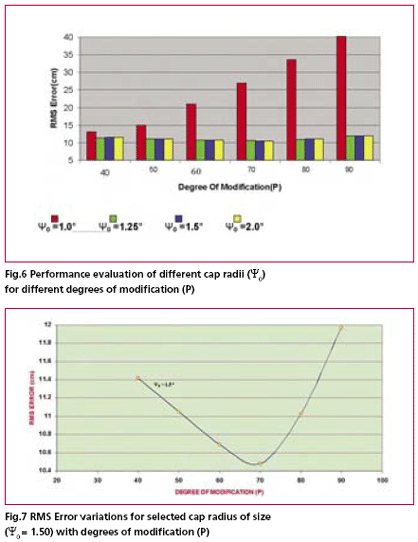
Analysis of results

A visual inspection of above figures give an idea about the extent of deviation of gravimetric geoid heights from GPS – levelling geoid heights. It could be well ascertained that optimum size of cap radius should be larger than 1° and degrees of modification should be around 60 – 70 for this particular region in order to achieve an optimum solution for gravimetric geoid. It is further argued that due to varying error characteristics of gravity data sources, different results can be expected in different regions. It has also been seen from the Fig. 6 that any value below 1° of cap radius result in comparatively worse fit due to numerical instability in the solution.

However, as size of cap radius approach close to 1.5 degree the solutions attain the stability as evident from the Fig. 6 wherein it is clearly shown that increase in size of cap radius beyond 1.5 does not improve the root mean square (RMS) error of differences between gravimetric (computed) and observed geoid heights. Thus the most appropriate size of cap radius is 1.5° for the given data and now only task remains to determine the optimum value for degree of kernel modification P. This is again done by plotting the RMS error against each corresponding degree of modification for fixed cap radius of size 1.5° (see fig. 7). Featherstone (2003) demonstrated that due to removal of the low – frequency Legendre polynomials the spheroidal (Wong and Gore) Kernel oscillates between positive and negative values and the oscillation increases with increase in degree of modification. The increased oscillation of the kernel induced numerical instability in solutions of Stokes Integral. However, it is not always necessary that the lowest of the low degree range gives better solutions. Considering these facts we testified the results starting with P=40 and allowed to vary in the step of 10 to evaluate the change in performance. The RMS error was taken as the standard parameter in order to select the optimum degree of modification. Fig. 7 clearly indicates that RMS error of the Least square fit is lowest for the solution derived using P=70 as degree of kernel modification.

The above illustrations gives an overview of the procedure to be adopted while deriving the optimum solution for gravimetric geoid. The GPS–leveling observations are of great help in this process and without it the quality assessment of gravimetric geoid solution can not be made with authenticity.

Conclusion

Rather than presenting simply the requirements of GPS – levelling data

only for comparison purpose this study has focussed its importance in deriving an optimized solution of gravimetric geoid. Wonge and Gore modification approach was examined and its performance was evaluated by changing size of cap radius and degree of modifications which is an arguably more informative exercise rather than making the geoid determination as routine computation. The problems that may be encountered when practically applying the modified kernels have been described. The case study has practically proved the optimisation procedure to be followed and importance of GPS–leveling data in this process. However, because of the pecularities of local gravity data error characteristics the modifications approach and its parameter might vary from region to region in practical gravimetric geoid computation

References

1. Evans, J.D., Featherstone, W.E. 2000. Improved convergence rates for truncation error in gravimetric geoid determination, Journal of Geodesy 74 (2), 239 – 248.

2. Featherstone. W.E., 2003, Software for computing five existing types

of deterministically modified integration kernel for gravimetric geoid determination. Computers and Geosciences, 29, 183-193.

3. Heck. B., Grüninger, W.,1987. Modification of Stoke’s integral formula by combining two classical approaches. Proceedings of the XIX General Assembly of the International Union of Geodesy and Geophysics, Vol. 2. Vancouver, Canada.

4. Heiskanen, W.H., Moritz, H., 1967. Physical Geodesy. W.H. Freeman & Co.., San Francisco, CA, 364 pp.

5. Lemoine, F.G., Kenyon S.C.,Factor, J.K., Trimmer, R.G., Pavlis, N.K., Chinn, D.S., Cox, C.M., Klosko, S.M., Luthcke, S.B., Torrences, M.H., Wang, Y.M., Williamson, R.G., Pavlis, E.C., Rapp, R.H., Olson, T.R., 1998, The development of the joint NASA GSFC and the National Imagery and Mapping Agency (NIMA) geopotential model EGM 96, NASA/TP –1998- 206861. National Aeronautics and Space Administration Maryland, USA, 575pp.

6. Molodensky, M.S., Eremeev,V.F., Yurkina, M.I.,1962. Methodes for study of the external gravitational field and figure of the Earth. The Israeli Programme for the translation of Scientific Publications, Jerusalem, Israel, 248 pp.

7. Nagarajan,B.,1994.Definition and realization of a global vertical Datum,Report N0.427,Deptt. Of Geodetic Science ,The Ohio State University,Columbus,Ohio.

8. Nagarajan, B., Singh, S.K.,, 2005. On the Derivation of Orthometric Heights from GPS-Levelling Observations. GIS Development, 9(4).

9. Stokes, G.G., 1849. On the variation of gravity on the surface of the Earth. Transaction of Cambridge Philosophical Society 8, 672-695.

10. Vanic~ek P., Sjöberg, L.E., 1981. Reformulation of Stoke’s theory of higher than second-degree reference field and modification of integration Kernels. Journal of Geophysical Research – Solid Earth 96 (B4), 6529 – 6539.

11. Vanic~ek P., Featherstone, W.E., 1998. Performance of three types of Stoke’s Kernel in the combined solution for the geoid, Journal of Geodesy 72 (12), 684-697.

12. Vanic~ek P., Kleusberg, A., 1987. The Canadian geoid- Stokesian approach manuscript a geodaetica 12 (2), 86-98.

13. Wong L., Gore, R., 1969. Accuracy of geoid heights from modified Stokes Kernel, Geophysical Journal of the Royal Astronomical Society 18, 81-91.