A Case study on PPP kinematic and RTK positioning methods in Urban Environment

A case study has been executed for obtaining the PPP Kinematic and RTK positioning results

Raghupati Shukla PhD student, Curtin University, Australia

Introduction contains sections of status about the GNSS satellites, back ground of GNSS–based positioning methods, Threats in positioning and description of faults.

Global Navigation Satellite System (GNSS)

The Global Positioning System (GPS) is currently main GNSS system used for positioning and navigation. The GNSS emerge for civilian use. These include Galileo (European Union in cooperation with European Space Agency), BeiDou (China), Global Navigation Satellite System (GLONASS); and the Japanese regional augmentation systems such as Quazi-Zenith Satellite System (QZSS) (Japan) and the Indian Regional Navigation Satellite System (IRNSS). For GPS, the Block IIF GPS satellites, of which two are in operation, are delivering carrier signals on a new civil frequency, L5 centred at 1176.45MHz, in addition to the existing dual frequency carriers, L1 (1575.42 MHz) and L2 (1227.60MHz) (Cao et al., 2010). The Block IIR-M satellites, seven of which are in operation, are delivering a civilian code on the L2 carrier, namely the L2C. Future Block III satellites will transmit a new civil code on the L1 carrier, namely L1C. GLONASS is currently fully operational and is being modernized to transmit triple-frequency signals using Code Division Multiple Access (CDMA), from Glonass-K1 satellites. BeiDau currently has 15 operational satellites with a regional coverage over Asia–Pacific region with satellites transmitting signals on three frequencies: B1 at 1561.098MHz, B2 at 1,268.52 MHz and B3 at 1,207.14 MHz (Hauschild, Steigenberger, & Rodriguez- Solano, 2011). Galileo signals are delivered on four frequency bands, namely E1 at 1575.42 MHz, E5a at 1176.45 MHZ, E5b at 1207.140 MHZ and E6 at 1278.45 MHz (Hein et al, 2001). The first QZSS satellite was launched on 11 September 2010, and is transmitting signals on the three GPS frequencies as well as fourth carrier frequency (E6), LEX, on 1278.75 MHZ (Sawamura et al, 2001). The first IRNSS was launched in 2015 and has one operating frequency on the L1 band.

GNSS-based Positioning algorithms (PPP, RTK and NRTK)

The GNSS-based positioning methods typically used in land applications such as (i) precise point positioning (PPP) (ii) realtime kinematic (RTK) and (iii) Network RTK. Some of their characteristics are summarised in the following.

PPP is a method that utilize precisely available satellite orbit and clock correction data to perform absolute positioning using measurement from a single GNSS receiver (Rizos, Janssen, Roberts, & Grinter, 2012). PPP requires a long convergence time of approximately 30 minutes to achieve decimetre-level accuracy and several hours to achieve cmlevel accuracy, which makes it impractical for most real-time applications (Bisnath & Gao, 2009). The main factors which cause the long convergence time include the high noise amplification of the code measurements, the number and geometry of satellites tracked, user environment, and dynamics and measurement quality. In case of ionosphere correction and ambiguity resolution, it is possible to reduce the convergence time of PPP to 10 cm horizontal accuracy (Banvile & Langley, 2012; Banville, Collins, Zhang, & Langley, 2014; Chen & Gao, 2008).

The observation equations for the carrier-phase and pseudorange measurements, from a GNSS satellite, s, to receiver, r, on frequency, j, are as follows (Odolinski et al, 2014).

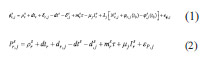
The PPP observation equations require precise error modeling. PPP solution is sensitive to errors in the used or computed values of the following: (i) precise satellite clock corrections (ii) satellite antenna phase center offset (iii) satellite antenna phase center variations (iv) precise satellite orbits (v) code and phase biases (vi) relativity term (vii) satellite antenna phase wind-up (viii) receiver antenna phase center offset (ix) receiver antenna phase center variations (x) receiver antenna phase wind-up (xi) solid earth tide displacements (xii) ocean loading (xiii) polar tides (xiv) plate tectonic motion (xv) tropospheric delay and (xvi) ionosphere delay. Errors in these parameters will have a direct impact on integrity and positioning performance.

Real Time Kinematics (RTK) is a technique which provides high positioning performance in the vicinity of a base station. The technique is based on the use of carrier measurements and the transmission of corrections from the base station. RTK is a technique that applies differential positioning, where a rover receiver receives measurements corrections from a reference station to cancel atmospheric, orbital and satellite clock errors in the measurements. RTK can achieve centimeter positioning accuracy for short baseline from the reference station under different operational conditions (open sky, partially blocked sky) (Kashani, Grejner- Brzezinska, Wielgosz, & Wielgosz, 2005; Kozlov & Tkachenko, 1998; Henkel & Gunther, 2012; Kim & Langley, 2007; De Jonge, Tibernius, & Teunissen, 1996). Two types of RTK techniques are available: local RTK (using a single reference station) and network RTK (using multiple reference station).Local RTK has a limitation where the distance dependent errors will be significant when the baseline exceeds 15km.In network RTK, Continuously operating referenced station (CORS) network is used to reduce the number of reference station can reach tens of kilometers NRTK GPS observation data are supplied to users via the Internet and are able to support high-accuracy position requirements. However, few of the issues affecting the performance of NRTK are (i) ionosphere delay (ii) ambiguity resolution (iii) error in computing network corrections (v) communication method between the network and the user. These errors have an impact on integrity and positioning performance of the system.

PPP Kinematic and RTK positioning results (Post Processing)

A case study has been executed for obtaining the PPP Kinematic and RTK positioning results. An R10 GNSS receiver was mounted on roof top of the car. The figure 1 and 2 shows trajectory of the car from Curtin University to Perth central area where high rise buildings are located. A total running time of the car was 01:25:55.

Three different softwares have been used to analyse the results of PPP kinematic and RTK algorithms such as (i) Canada Centre for Remote Sensing (CSRS-PPP) (ii) Magic GNSS (iii) Trimble software.

Simulation of CSRSPPP software

The table 1 shows input parameters for processing CSRS-PPP software. The figure 3 shows pseudo range residuals sky distribution.

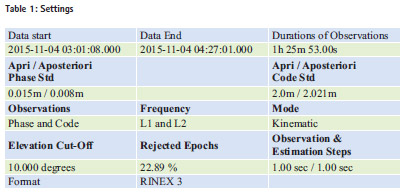
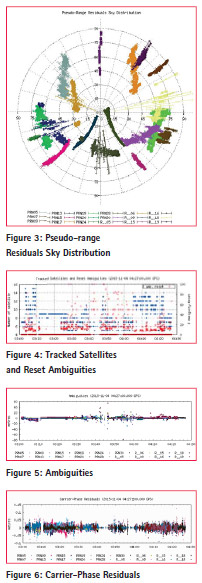
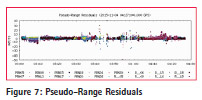
The figure 4 shows tracked satellite and reset ambiguities. The figure 5, 6 and 7 shows ambiguities, carrier phase residuals and pseudo range residuals respectively. The ambiguities are fluctuating between -5 to 5 m with respect to time. Lesser is the number of satellites, more are the ambiguities found in the figure.

The figure 8 shows standard deviation of the geodetic coordinates with respect to the time.

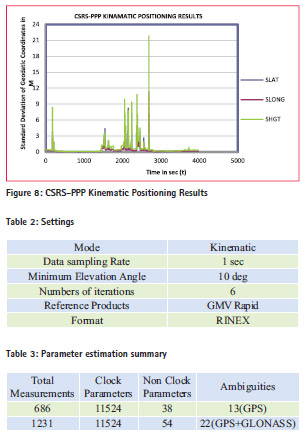
Simulation of Magic GNSS software

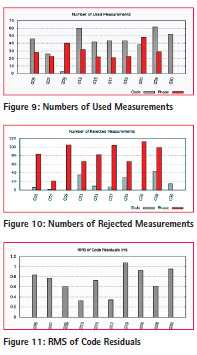
Magic GNSS was used for two scenarios such as 1) GPS only 2) (GPS+GLONASS) Table 2 and 3 shows the settings of Magic GNSS software and Parameter estimation summary. The figure 9 and 10 shows the numbers of used and rejected parameters for GPS case. It can be seen that Go5 has used more numbers of code measurements compare to phase measurements. And G09 has used more numbers of phase measurement compare to code measurements. The figures 11 and 12 show RMS of Code and Phase residuals.

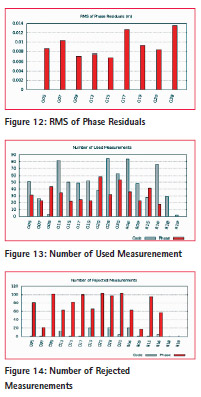
The figure 13 and 14 shows the number of parameters used and those rejected for GNSS case. The figure also shows that more measurements are available for GNSS rather than GPS and similarly more ambiguities are presents in case of GNSS compared to only GPS.

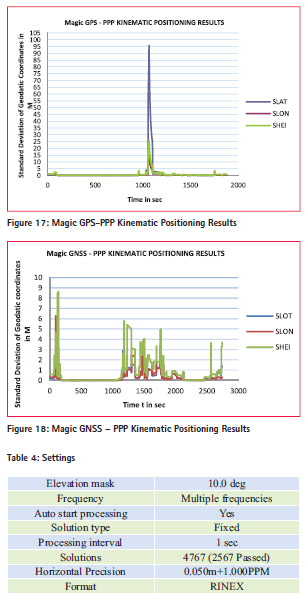
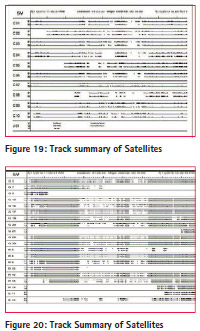
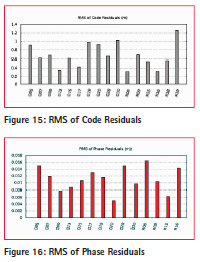
The figure 15 and 16 shows RMS of Code and Phase residuals. deviation of geodetic coordinates with respect to time for Magic GPS and Magic GNSS. These figures are the proof that Continuity can be improved by using multi constellation system rather than use of one constellation.

Simulation of Trimble software

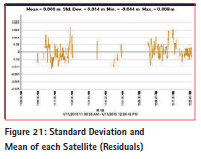
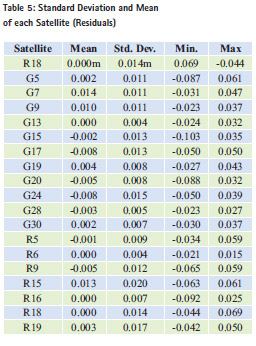
Trimble software has been used for getting RTK (Real-time Kinematic) positioning results. Table 4 shows settings of the Trimble software. The figure 19 and 20 shows track summary of all the satellites such as (i) GPS (ii) Beidau (iii) GlONASS (IV) QZSS. Only two satellites are available throughout the time and rest of the satellites have signals blocked for some time duration. Figure 21 shows residuals of each satellite with their standard deviations and means. Table 5 shows standard deviation and mean of each satellite.

This research case study proved that Trimble software achieves cm level accuracy by using RTK method. The Magic GPS gives more accurate positioning results compared to the Magic GNSS in PPP kinematic method. However, continuity is better achieved in case of Magic GNSS compared to the magic GPS in PPP kinematic method. The Magic software achieves more accurate positioning result than CSRS-PPP and CSRSPPP achieves more continuity compare to the Magic software.

Total epochs are 5155. Out of these total epochs, the Trimble software processed 2567, the CPRS-PPP software processed 3976 and Magic software processed 2739 epochs. The rejected epochs are the result of a signal blockage, poor satellite visibility and insufficient measurements to calculate positioning. (Sample rate 1 sec).

Conclusion

The case study presented shows that good software like Magic, CSRSFigure PPP and Trimble can achieve 70% availability to target applications such as (i) Ambulance tracking (ii) Fire Brigade (iii) Machine Automation with Metre to Cm level accuracy and using PPP-kinematic and RTK methods. However, signal blockage, poor satellites visibility and insufficient measurements can reduce availability to achieve target application. It is also shown that integration of other navigation technology like Locata and inertial navigation technology is an option to increase availability for required target application. The future work of this research is to implement a case study using GNSS-Locata receiver and by using PPP-Kinematic method to increase availability for required target application.

Acknowledgement

I would like to specially thank Mr. Carl Lares (Technical Officer) for helping me with executing the case study.

References

Banville, S., & Langley, R. B. (2010). Instantaneous Cycle-Slip Correction for Real-Time PPP Applications. Navigation, 57(4), 325- 334. doi: 10.1002/j.2161- 4296.2010.tb01786.x.

Banville, S., Collins, P., Zhang, W., & Langley, R. B. (2014). Global and Regional Ionospheric Corrections for Faster PPP Convergence. Navigation, 61(2), 115- 124. doi: 10.1002/navi.57.

Bisnath, S. B., & Gao, Y. (2009). Innovation: Precise point positioning.

Cao, W., Hauschild, A., Steingenberger, P., Langley, R. B., Urquhart, L., Santos, M., & Montenbruck, O. (2001, October). Performance evaluation of integrated GPS/GIOVE precise point positioning. In Proceedings of the 2010 International Technical Meeting of The Institute of Navigation (pp. 540-552).

Chen, K., & Gao, Y. (2008). Ionospheric Effect Mitigation for Real-Time Single- Frequency Precise Point Positioning. Navigation, 55(3), 205-213. doi: 10.1002/j.2161-4296.2008.tb00430.x

Crews, M. (2007). GPS Wing Program Update. Munich Satellite Navigation Summit. Datta-Barua, S., Walter, T., Blanch, J., & Enge, P. (2008). Bounding higher-order ionosphere errors for the dual-frequency GPS user. Radio Science, 43(5).

De Jonge, P., Tibernius, C., & Teunissen, P. (1996). Computational aspects of the LAMBDA method for GPS ambiguity resolution. Paper presented at the PROCEEDINGS OF ION GPS

Hauschild, A., Steigenberger, P., & Rodriguez-Solano, C. (2012). Signal, orbit and attitude analysis of Japan’s first QZSS satellite Michibiki. GPS solutions, 16(1), 127-133.

Hein, G. W., Godet, J., Issler, J. L., Martin, J. C., Lucas-Rodriguez, R., & Pratt, T. (2001, September). The Galileo frequency structure and signal design. In Proc. of ION GPS (Vol. 2001).

Henkel, P., & Günther, C. (2012). Reliable Integer Ambiguity Resolution: Multi-Frequency Code Carrier Linear Combinations and Statistical A Priori Knowledge of Attitude. Navigation, 59(1), 61-75.

Jokinen, A., Feng, S., Milner, C., Schuster, W., Ochieng, W., Hide, C., … & Hill, C. (2011). Precise Point Positioning and Integrity monitoring with GPS and GLONASS. In European Navigation Conference (Vol. 2011).

Kashani, I., GREJNER-BRZEZINSKA, D. O. R. O. T. A., & Wielgosz, P. (2005). Toward Instantaneous Network-Based Real-Time Kinematic GPS over 100 km Distance. Navigation, 52(4), 239-245.

Kim, D., & Langley, R. B. (2007). Ionosphere-Nullification Technique for Long-Baseline Real-Time Kinematic Applications. Navigation, 54(3), 227-240.

Kozlov, D., & Tkachenko, M. (1998). Centimeter-Level, Real-Time Kinematic Positioning with GPS+GLONASS C/A Receivers. Navigation, 45(2), 137-147.

Murphy, T., Geren, P., & Pankaskie, T. (2001, July). GPS Antenna Group Delay Variation Induced Errors in a GNSS Based Precision Approach and Landing Systems. In Proceedings of the 20th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2007) (pp. 2974-2989).

Odolinski, R., Odijk, D., & Teunissen, P. J. (2014). Combined GPS and BeiDou instantaneous RTK positioning. Navigation, 61(2), 135-148. doi: 10.1002/navi.61.

Rizos, C., Janssen, V., Roberts, C., & Grinter, T. (2012). PPP versus DGNSS. Geomatics World, 20(6), 18-20.

Sawamura, T., Takahashi, T., Moriguchi, T., Ohara, K., Noda, H., Kogure, S., & Kishimoto, M. (2001, December). Performance of QZSS (Quasi-Zenith Satellite System) & L-Band Navigation Payload.