| Geodesy | |
Optimizing gravimetric geoid solution
|
||||
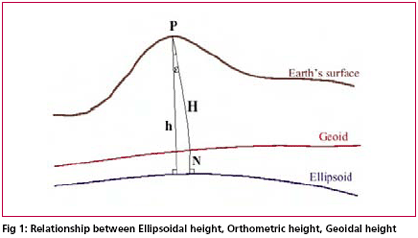
| Transformation of GPS derived ellipsoidal height to orthometric height is one of the most important applications of gravimetric geoid. Its applicability remains questionable if the above transformation cannot be done to a reasonable order of accuracy. Use of GPS observations at levelling benchmarks and subsequently determined geoidal seperation using the geometrical relationship between geoid and ellipsoid (see fig. 1 ) serve as standard for accuracy assessment of gravimetric geoid. Stokes’s (1849) solution of geodetic boundry – value problem requires a global integration of gravity anomalies to compute the separation (N) between the geoid and geocentric reference ellipsoid.
In any gravimetric geoid computation at regional or local level the gravity data only to the extent of region of interest is inevitably used. The Stokes integral formula which is generally used to provide the gravimetric geoid solution, requires a global integration of surface gravity anomaly data over the entire Earth. However, this requirement is practically difficult to meet due to the reasons of security and political sensitivity, the integrations is performed over a limited spherical cap, which is bounded by the spherical distance This practical approach usually result in errors what has been called as truncation error (Molodensky et.al., 1962). In any gravimetric geoid computations at a regional or local level the gravity data only to a limited extent is used, therefore Stokes formula in its original form may not provide the desired solution. This truncation error can be treated as a remote – zone contribution and computed using the spherical harmonic expansion of the coefficients that comprises a global geopotential model (Evans & Featherstone, 2000). Since such models are available only to an expansion of 360 degrees the truncation error remains due to omission of the higher degree terms. In order to reduce the effect of these errors and influence of other potential resources and also to attain the geoid solution which is best fit to the geometric geoid computed from GPS – Levelling observations at discrete points, an appropriate modification to Stokes kernel and an optimum value of spherical cap radius over which the integral will actually performed are the most desired quantities. This will allow for the best estimate of geoid height to be made from an approximated (i.e. truncated at Basic theory of Gravimetric Geoid ComputationRemove – compute – Restore (RCR) type of estimator using appropriate modification of Stokes integral kernel is the most popular technique of regional or local gravimetric geoid computation in preset scenario. The RCR technique invariably utilized the global geopotential model’s potential coefficients viz. EGM96 to remove the long wavelength effect from the local terrestrial gravity data at the remove stage which is added back to the geoid height computed from residual gravity data using Stokes Integral at the restore stage. The reference global geopotential model (GGM) usually provides long-wavelength information of Earth’s gravity field whereas the local/regional terrestrial data such as gravity anomalies supplement this information with the short wave-length geoid information to get the reasonably accurate gravimetric geoid for the region of interest. The combination of these kind of data sources for determination of geoid height N has been termed as generalized Stokes scheme for geoid computation (Vanic~ek and Sjöberg, 1991). According to the scheme the long wave length contribution of a GGM viz. EGM96 (NM) are corrected to a certain extent by a global integration of residual gravity anomalies to get the geoid height (N1) at the computation point by the expression As already explained it is impractical to evaluate the integral of equation over the entire earth due to the various constraints associated with data availability it is preferred to perform the evaluation in a domain of predefined spherical cap of radius To circumvent effect of leakage of errors in geoid model solution the ideas of using an appropriate modification of the original Stokes kernel along with optimum value of spherical cap radius Optimisation process of gravimetric geoid solutionThe Stokes kernel to a great extent forms a weighted integral function for gravity data in geoid model solution given by numerical solution of Stokes integral. This strong dependence of the geoid computation and associated errors on the kernel is the basis for any kernel modifications, the objective being to reduce the error. Since the basic purpose of determination of geoid is to transform the GPS derived ellipsoidal heights (h) to orthometric heights ( H ) using the relationship; h=N+H, the most appropriate form of kernal modification and optimum size of the cap radius is determined empirically on trial and error basis. Choice of kernel modificationsThe approaches of kernel modifications are broadly classified into two categories, deterministic and stochastic, The stochastic approach essentially requires the error characteristics of local gravity data and global geopotential model which is not known to a satisfactory level in most of the cases and hence are of limited practical applications. The deterministic approaches presented by Wong and Gore (1969), Heck and Grüninger (1987) and Vanic~ek Kleusberg (1987) are more frequently used in geoid computation and hence considered to be potential alternatives. All these approaches are related to each other in general as by making certain changes one’s expression degenarates to the other the origin being the simple approach presented by Wong and Gore (1969) which involves removing the low – degree terms from the original kernel, according to: Accuracy of computed geoid undulations depend largely on the extent of the terrestrial gravity anomaly data used around the computation point. Nagarajan (1994) has shown that due to propagation of error with increase in the cap radius beyond certain value ,does not improve rather degrades the geoid undulation results.The choices of size of the cap radius and approach of kernel modifications are strictly region dependent and till today no approach is claimed to be an ideal one which can straightway be used irrespective of the size and location of the area of interest. Therefore it is rather difficult to make the choice of most suitable kernel modification approach or size of the cap radius unless the geoid results are compared with the GPS – levelling observations results thus making it an essential component of gravimetric geoid computation process. Case studyGPS-levelling and gravimetric geoidIn order to illustrate the procedure to achieve an optimized solution for gravimetric geoid the free air gravity anomaly data from Bangalore and adjoining region in a block of 2° X 1° was taken for computation. The RCR technique implemented in generalized Stokes scheme was adopted and contribution of EGM96 (Lemoine. et.al.) global geopotential model to degree and order of 360 was removed from the observed gravity data. A local DEM was also developed based upon the available height data in the region and terrain effect was removed from the reduced gravity anomaly data. The complete procedure is not explained here as the study is focussed on selection of most appropriate size of cap radius and approach of kernel modification to derive the gravimetric geoid solutions which is best fitted in least square sense to the geometric geoid derived from GPS observations at levelling bench marks. GPS observations at about 84 leveling bench marks were carried out by Geodetic & Research Branch, Survey of India, as a part of project undertaken to provide Ground Control Points (GCPs) to develop a comprehensive development Plan for Bangalore City (See Nagarajan and Singh, 2005 ). Out of these 84 points 68 points were selected for performing a realistic assessment of geoid model and subsequently optimized the integral parameters of Stokes Formula. In order to avoid the complexity in comparison of different geoid solutions correspond to different modification approaches with geometrically derived geoid heights from GPS-leveling observations, we have chosen the most widely used Wong and Gore (1969) approach and geoid solutions were obtained by varying size of cap radius ( ?0 ) and degree of modification P. For each typical combination of cap radius and degree of modification the fitting of gravimetric geoid heights to observed GPS – Leveling height differences at discrete points has been analysed and statistics of differences were computed. Fig. 2 to Fig. 5 represents the fit of gravimetric geoid heights to geometric geoid heights for different combinations. |
||||
Pages: 1 2













 (No Ratings Yet)
(No Ratings Yet)




