| GNSS | |
Simulation of Galileo E5 Signal
|
Fantinato Samuele |
|||||||||||||||
|
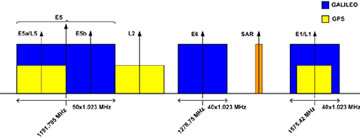
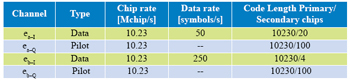
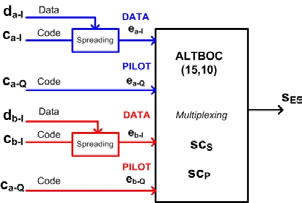
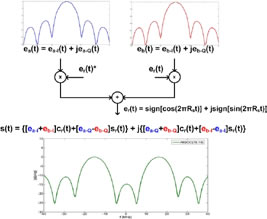
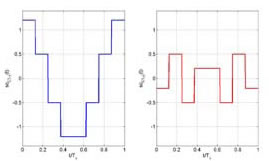
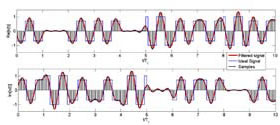
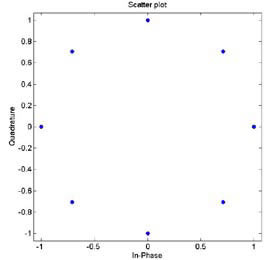
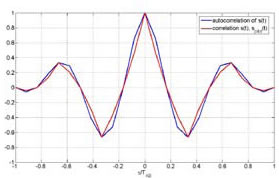
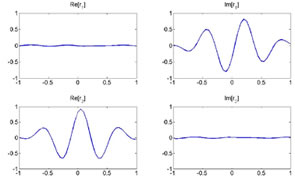
In Galileo AltBOC has been modified introducing two different subcarriers and the products of the components in order to obtain a signal that lies on an 8-PSK constellation (constant envelope) which is very important for satellites high power amplifiers. Figure 3 Construction and Power Spectral Density of AltBOC Signal Figure 5 Real and Imaginary part of E5 ideal signal, E5 filtered signal and its samples (K=8) Figure 5 Real and Imaginary part of E5 ideal signal, E5 filtered signal and its samples (K=8) Figure 6 Constellation of E5 signal Figure 7 Shapes of autocorrelation of S(t) and correlation between S(t) and Spilot(t) In the following lines is reported how, in the simulation, the samples of E5 signal are generated, for more details see [11]. As known in AltBOC(n, m), n represent the chip rate of the signal and m the frequency of the subcarriers. As one can see the subcarrier period is Ts = (n/m) Tc = (2/3)Tc. The two subcarriers are defined every Ts/8, so after the multiplexing scheme each chip period is composed of N = 12 slots in which the values of the signal can be different. The components ex– Y(nTc) are then interpolated with a “hold interpolator” of factor N = 12 and so directly multiplexed according to the expression of Eq. 2. The output signal is defined in TAB = Tc/12. Figure 8 Shapes of correlations r1(t) and r2(t) Acquisition, Tracking and Data RecoveryAs previously said it has been developed a receiver for the demodulation of the overall E5 signal: the signal in input at the receiver is directly sampled (in a simulation the signal is already sampled) and the complex samples are then processed. In the acquisition and tracking process is performed a correlation between the received sampled signal and the samples of a local AltBOC(15,10) pilot signal defined as: Eq.4 This signal can been obtained from Eq. 2 setting to zero the data components ea–I and eb–I and the different normalization factor is introduced in order to not reduce the peak of correlation. In figure 7 one can observe that there is no a significant difference between the autocorrelation of S(t) signal and the correlation between S(t) and Spilot(t). The acquisition is performed using FFT based technique [4] and the delay and doppler frequency are estimated with precision depending on the sample time Tsamp and on the length of correlation. Also for the tracking of the signal the correlation is between the received signal and pilot signal of Eq. 4. For the tracking it is implemented a non-coherent Early minus Late DLL [6]. ConclusionIn this paper have been described the main features of Galileo E5 signal and some algorithms for signal generation and software receivers. In particular have been highlighted differences between conventional AltBOC and that used in Galileo: two subcarriers are used and the signal has an 8-PSK constellation. Have been given some useful equations for the implementation of a signal generator or the development of a simulation and have been proposed some techniques for the acquisition, tracking and data recovery of the overall received signal. References[1] ESA,GJU “Galileo Open Service: Signal In Space Interface Control Document (OS SIS ICD) Draft 0’’, 23-05-2006
|
|||||||||||||||
|
|||||||||||||||
|
Pages: 1 2


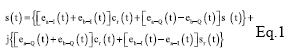
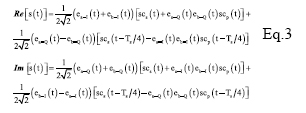











 (No Ratings Yet)
(No Ratings Yet)




