| GNSS | |
Low-cost multiband GNSS receiver and their performance in accuracy
This study aim is to investigate the possibility to used low cost GNSS receiver in the place of those costly one, by appreciating the time of processing data and the coordinates |
|
|
|
|
|
Abstract
The high cost of modern GNSS (Global Navigation Satellite System) receiver and their post processing software present an obstacle in the surveyed laboratories for poor countries. This study aim is to investigate the possibility to used low cost GNSS receiver in the place of those costly one, by appreciating the time of processing data and the coordinates to converge under 50 seconds, then model the errors between those two instruments before evaluating their accuracy. The materials used were the one of reading, and observation of data, the order for the processing of data. The method consisted to carry out data by the static PPP (Precise Point Positioning) and the dynamic method (Kinematic PPP) and PPK (Post Processed Kinematic) of 10 benchmarks SEPRET (Société d’Etude des Projets et de Réalisations des Travaux) pilars through two multiband GNSS receivers Emlid Reach RS2.

1. Introduction
The Global Navigation Satellite System (GNSS) has been widely used for many years because it provides precise positioning (Omer F. et al., 2021). Also has been used for various navigation (air, water, road transport, earth observation, weather forecasting timing and national coordinate systems) and monitoring engineering structures, naturals hazards, surveying and others purposes (Tsakiri, M., et al., 2017; Lipatnikov, L., et al., 2019; Leick, A., et al., 2015; Teunissen, P.J.G., et al 2017; Guo, L., et al., 2017; Biagi, L., et al., 2016; Wang, S., et al., 2022).
Traditionally, they were obtaining positioning with GNSS using at least two receivers. The collected data were processed for highly accurate positioning by using the GNSS data processing software (Muchammad M., 2020). Those GNSS use Differential methods for high accuracy through with high cost. Nowadays, Precise Point Positioning (PPP) is an enhanced single GNSS receiver user with a point positioning technique for code or phase measurements using precise orbits and clocks to adjust ionospheric effects in dual frequency Measurements by an ionosphere free combination (Ashraf F., 2018). But because of its low cost and large number of users, PPP takes the spotlight (Amr H. et al., 2017; Semler, Q., et al., 2019; Krietemeyer, A., et al., 2020; Hamza, V., et al., 2021; RomeroAndrade, R., et al., 2021; Hamza, V., 2020; Hamza, V., et al., 2021; Broekman, A., et al., 2021; Tunini, L., et al., 2020; Samboko, H. T., et al., 2022; Janos, D., et al., 2021; Läpädat, A.M., et al., 2021).
The Canadian Spatial Reference System (CSRS) Precise Point Positioning (PPP) service provides post-processed position estimates over the Internet from GPS observation files submitted by the user. Precise position estimates are referred to the CSRS standard North American Datum of 1983 (NAD83) or the International Terrestrial Reference Frame (ITRF). Single station position estimates are computed for users operating in static or kinematic modes using precise GPS orbits and clocks. The online PPP positioning service is designed to minimize user interaction while providing the best possible solution for the given observation availability. Currently, users need only to specify the mode of processing (static or kinematic) and the reference frame for position output (NAD83 (CSRS) or ITRF). The observations processes are selected from the submitted RINEX (Receiver Independent Exchange) file in the following order:
– L1 and L2 pseudo-range and carrier phase observations
– L1 pseudo-range observation An L1 pseudo-range only solution will be performed in case of failure of the L1 and L2 pseudo-range and carrier phase solution (Ashraf Farah, 2013).
RTKLib (Real Time Kinematic library) is an open-source program package for multiGNSS positioning software developed by Tomoji Takasu from the Tokyo University of Marine Science and Technology in Japan. RTKLIB can process collected data with standard and precise positioning techniques by using different satellite constellations, GPS, GLONASS, Galileo, QZSS, BeiDou and SBAS. It supports many positioning modes including DGPS/ DGNSS, Kinematic, Static, MovingBaseline, PPP-Kinematic, PPP-Static and PPP-Fixed modes (Ibrahim M., 2018).
The online service that will be used in the case of this study is CSRS-PPP because of its low-cost and it is the most precise free online service. The CSRS-PPP is taking into consideration only the GPS and GLONASS constellations due to the fact that the others constellations are not yet considered to be very stable.
RTKLIB software will equally be used in this study to convert our raw logs to RINEX format as it provides good and acceptable results and is equally free software.
At the societal level, this work will help the Ministry of State Property, Surveys and Land Tenure, the Ministry of Housing and Urban Development, and the Ministry of Public Works to take better decision in the georeferentiations of the parcels of lands in the process of obtaining land certificates and equally in the georeferentiation of public work projects. This work will equally facilitate developing countries in the process of equipping their research laboratories since they don’t have sufficient finance to buy highcost equipment. Also, the work elaborates on the resolution that can be obtained in the realization of the digital elevation model useful during the hydrologic and hydraulic modelling in the Tongo Bassa watershed.
From a scientific view, this work will give idea on the influence of accuracy and the duration of observations on the convergence behaviour using a multiband GNSS receiver with three common positioning techniques: static PPP, PPK mode and kinematic PPP in the equatorial zone of the earth globe. It will also:
Determine the required duration of readings to reach the convergence by employing the three different techniques and also give the relationship that exists between them in the equatorial zone using a low cost multiband GNSS receiver.
Draw the diagram of uncertainties (sigma 95%) in function of the observation lengths over the latitude, the longitude and the ellipsoidal height in static PPP; Study the average, the minimum, the maximum and the standard deviation of the uncertainties in static PPP over the three axes; Study the coordinates™ behaviour of the PPK and the Kinematic PPP techniques in function of the observation duration; Study the difference between the three observation technique coordinates and the benchmarks coordinates over the three axes; Draw the prediction curves existing between the three observation modes and the benchmarks.
During the project of densification of the geodetic network system in Cameroon, many benchmarks™ points of the first order, second order and third order have been coordinated using sophisticated and high-cost equipment. The high cost of these modern equipment is an obstacle in the survey laboratories of developing countries. The comparison study between the accuracy of low-cost and high-cost equipment where carried (Margaria, M., 2020; Nguyen, N.V., et al., 2021; Gabl, M and Heller, A, 2021), and also the relationship between the accuracy and the recording interval using single and dual frequency receivers (Ashraf, F, 2013; Odolinski, R., et al., 2020; Garrido-et M. S. et al., 2019) but not through a convergence behaviour.
The main objective of this research is to study the performance through accuracy of a low cost multiband GNSS receiver. More specifically, the study seeks to study the influence of the recording interval on the convergence behaviour, then model theirs errors and accuracy with benchmark SERPRET pillars. This will be realized by assessing the evolution of time interval during the reading.
To study the influence of the accuracy of the coordinates on the convergence behaviour. This will be realized by evaluating the difference between the reading value of the low-cost receiver and the benchmark.
2. Methodology
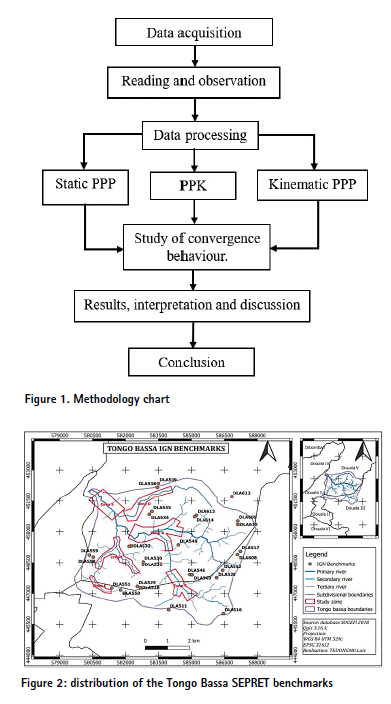
The present study has been done in the Tongo Bassa watershed following four steps which took place from March to September 2021 such as the collection of data, the reading and observation, the data processing, the evolution of the convergence of accuracy and the difference between the readings. Figure 1 gives all the steps of the methodology used to carry out this research study.
2.1. Data
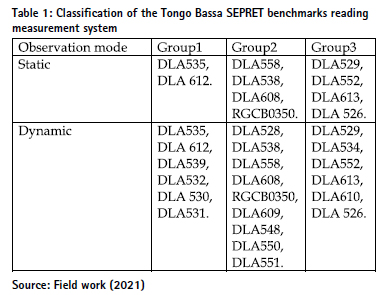
With a surface area of about 42 km², the area of study, the Tongo Bassa watershed is located in the Littoral Region of Cameroon which is in the Equatorial zone falling within the

2.2. Reading and observation materials
During the observations, we used:
Two multiband GNSS receivers Emlid Reach RS2 (the base and the rover).
A tripod BOCH BT 170 HD to keep our base stable;
A meter of 5m length to measure the pole height of our base station;
A smartphone Samsung Galaxy S8 having the android app ReachView installed in its system;
A field notebook well prepared to avoid the oblivion of any important information on the site.
Data processing materials:
The processing of the data is based for the majority on the software such as:
The online software CSRS-PPP;
The software package RTKLIB that has 3 main sections: RTKCONV, RTKPOST and RTKPLOT.
2.3. Methods
Classification of the benchmarks
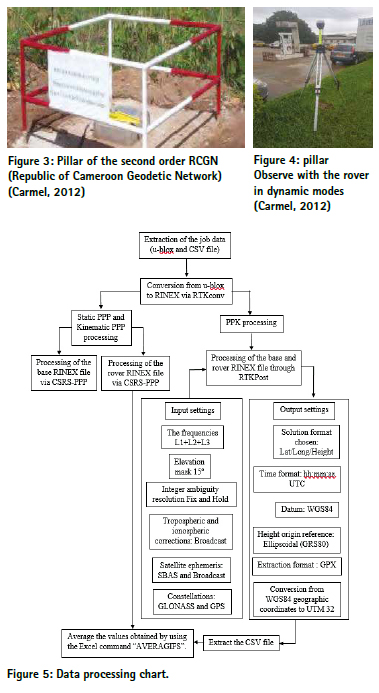
The benchmarks are classified in 3 groups according to the crowding of the environment where the benchmarks are located following the order given below:
Group1, for the most crowed environment with the presence of buildings or trees of more than 10m height at a distance of less than 50m around the beacon.
Group2, for the environment with the presence of buildings or trees comprised between 5 to 10m in height at a distance of less than 50m around the beacon.
Group3, for the environment without buildings or trees in a radius of 50m around the beacons, or with the presence of buildings or trees comprised between 0 to 5m in height at a distance of less than 50m around the beacon.
The table 1 classified the 21 benchmarks in function of the observation modes and the crowding of the environment in which they belong.
2.4. Data collection methods
During this step, the ReachView app connected to the base and the rover to create the daily job before starting the collection was used. The base and the rover were set to save data each 01 second with and elevation mask of 15°. The instrumental height was measured with our 5m length meter and set in the base and was equally noted on the field notebook.
PPP and PPK solutions were estimated using a multiband frequency L1/L2/L5 observations. And each static PPP-solution contains different lengths of observation duration (10 min., 20 min., 30 min, 45 min., 1 hr., 1.5 hrs., 2 hrs., 2.5 hrs., and 3 hrs.). Kinematic PPP and PPK solutions contain a length of observation of 50 seconds. Management of observations files was done using the software RTKLIB. The different sets of observations were processed and the PPP solutions were estimated through Canadian Spatial Reference System (CSRS) Precise Point Positioning (PPP) service (CSRS-PPP, 2013) and PPK solutions were estimated through RTKLIB since the coordinates of the base was already known. The chosen total length of observations was about 3 hrs. for the static PPP mode.
2.5. Data processing method
The data processing method is summarized in the figure 5.
3. Results and discussions
3.1. Convergence Accuracy Value Tendance According to the Recording Interval
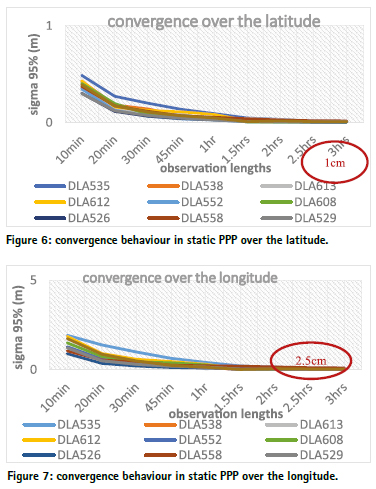
Sigma 95% in function of the observation lengths in static PPP. Figures 6, 7, 8 and 9 present respectively the convergence behaviour of sigma 95% in function of the observation lengths in static PPP mode over the latitude, the longitude, the ellipsoidal height and over the three-dimensional axes.
We can observe on the above figures that after 10 minutes of observation in static PPP, the value of sigma 95% is ranged within 130cm and 285cm. After 3 hours of observations, the values of sigma 95% for the 10 points surveyed become constants with an average value of 55mm. We can therefore conclude that static PPP over the latitude, the longitude, the ellipsoidal height and the three-dimensional axes converges respectively towards the values 10mm, 25mm, 45mm and 55mm after about 3 hours of observations with a lowcost GNSS multiband receiver in the equatorial zone.
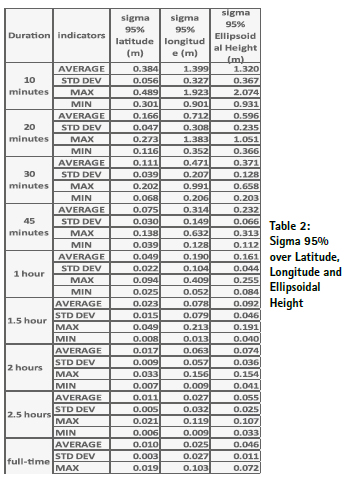
Table 2 gives for each of the points surveyed in static PPP the average of the uncertainties, the standard deviation, the maximum and the minimum of sigma 95% in function of the observation lengths over the latitude, the longitude and the Ellipsoidal Height.
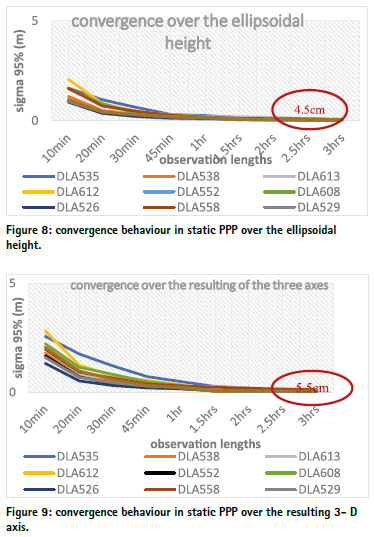
It shows that in static PPP, we reach centimetre level accuracy after about 3 hours of observations on the latitude, longitude and ellipsoidal height. This study is in perfect accordance with the results of Ashraf Farah on the study of convergence behaviour of static PPP (ASHRAF F., 2013), our observations with the receiver Emlid reach RS2 which is a three-frequency receiver converge faster than those of TOPCON GR3. They are equally in accordance with the results of Margaria Marie who found out that the receiver Emlid reach gives more accurate results than the receiver Trimble R8 (Margaria M., 2020). This might be due to the fact that the receivers Trimble R8 and Topcon GR3 are dual frequency receivers.
Behaviour of coordinates as a function of recording time in PPK and kinematic PPP
Figures 10, 11 and 12 present the behaviour of point DLA535 respectively over x, y and z axis in PPK mode and figures 13, 14 and 15 present also the behaviour of point DLA535 in kinematic PPP after 50 seconds of observations. The coordinates over X, Y and Z axes varied respectively within the ranges of 2.5cm length, 3cm length and 3cm in PPK; and 12cm length, 13cm length and 7cm length in kinematic PPP. The observations in PPK converge faster and are less mode disperse than those in kinematic PPP.
This is due to the fact the observations in kinematic PPP does not take into consideration the corrections of the base of the receiver and also there is no fix receiver used by CSRS-PPP around our area of survey to minimize the errors of the observations.
3.2. Errors Values Difference between the Benchmark and the Reading Coordinates
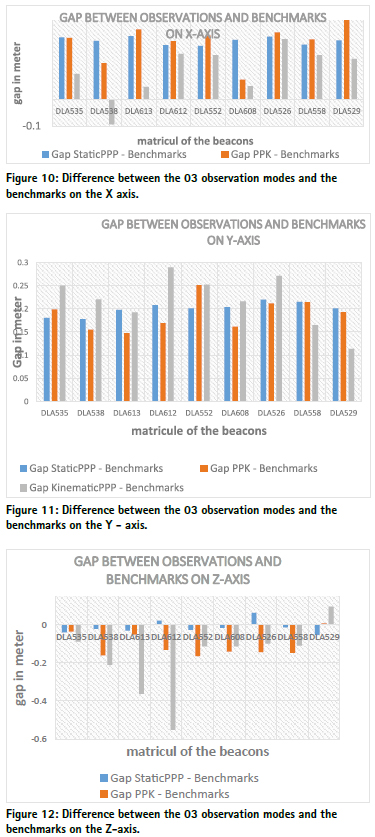
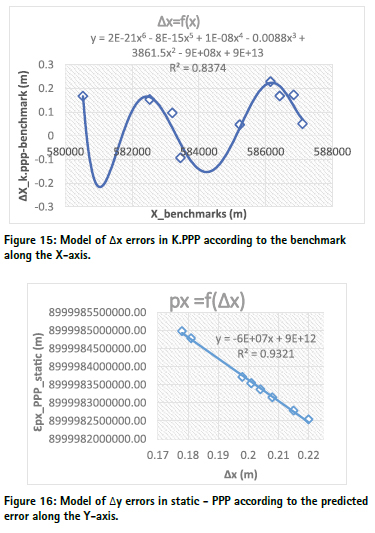
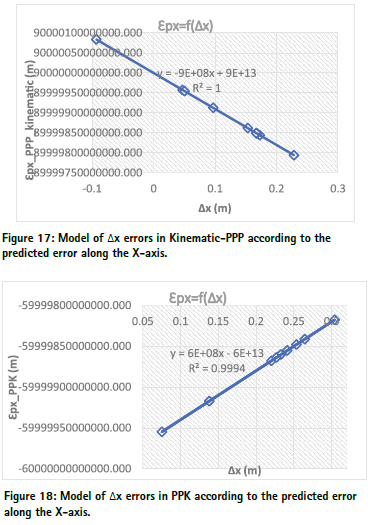
Difference between the 03 observation modes and the benchmarks. The figures 10, 11 and 19 present the differences of the reading between the static PPP and the benchmarks, the PPK and the benchmarks, and the Kinematic PPP and the benchmarks respectively on the X-axis, Y-axis and Z-axis.
3.3. Modeling of the Variation of Reading Values According to the Benchmark Coordinates of Beacons
The static PPP solutions are more related to the benchmarks than the PPK and the kinematic PPP solutions with a relative maximum difference of 5cm in the X, Y and Z-axis.
The kinematic PPP coordinates of the points DLA538 and DLA612 respectively along the x and z axes are systematically closer to the corresponding benchmarks for DLA538 and farer for DLA612 than the other points due to the static PPP solutions are more related to the benchmarks than the PPK and the kinematic PPP solutions with a relative maximum difference of 5cm in the X, Y and Z-axis.
The kinematic PPP coordinates of the points DLA538 and DLA612 respectively along the x and z axes are systematically closer to the corresponding benchmarks for DLA538 and farer for DLA612 than the other points due to the fact that the beacons DLA538 and DLA612 belong to group1. Meaning there are building or trees of more than 10m height at a distance of less than 50m around the beacon. We can therefore understand that the accuracy of observations with a low-cost multiband GNSS receiver depends of the sky visibility which is in accordance with the results obtained by AYHAN Ceylan, et al. in 2015 evaluating the Performance of Kinematic PPP and Differential Kinematic Methods in Rural and Urban Areas (AYHAN Ceylan, et al., 2015).
Relationship between the reading measurements and the benchmarks. The figures 13, illustrate respectively the relationships between ΔX (the difference between the coordinates of the observations in static PPP mode and the benchmarks over the axes X, and the benchmarks over X, -axis. The (1) equations of the trend lines of ΔX in function of the benchmarks over X. The values of R-squared are respectively equal to 0.9007, 0.858 and 0.5578 over X, Y and Z. this simply means that the relationship between the differences delta and the corresponding benchmarks is polynomial of 6th other and are more linked over the X-axis than over the Y-axis, and also more linked over the Y-axis than over the Z-axis.
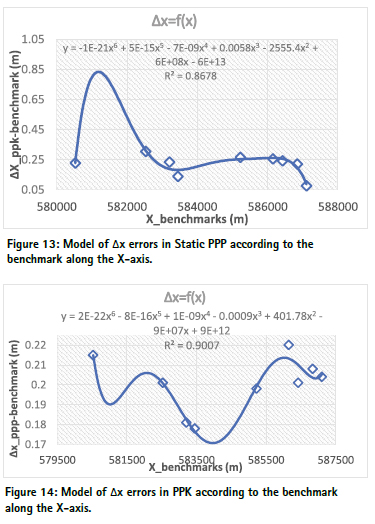
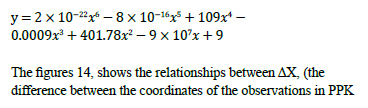

Modelling of the different delta errors according to the


4. Conclusion
The work aimed at studying the influence of the accuracy and the duration on the convergence behaviour using low cost multiband GNSS receiver. We started by studying the influence of the recording interval on the convergence behaviour using a low-cost receiver and then the impact of accuracy on the convergence using a lowcost GNSS receiver. We did 172 readings in kinematic mode (kinematic PPP and PPK) and 10 readings in static mode using the multiband GNSS receiver Emlid Reach RS2. The PPK readings gives better accuracy than kinematic PPP readings and the difference between the PPK coordinates and the benchmarks is ranged within [7.5cm – 30.4cm], [14.8cm – 25.2cm] and [-16.5cm – 0.8cm] respectively over the X, Y and Z-axis. PPK survey can be used in many surveying applications such as: cadastral survey, road construction survey, realization of DEM for hydrologic and hydraulic modelling. While the difference between the Kinematic PPP coordinates and the benchmarks is ranged between [-9.3cm – 22.8cm], [11.4cm – 29cm] and [-55.2cm – 9.6cm] respectively over the X, Y and Z-axis. Kinematic PPP survey can show itself important in the applications such as agriculture, forestry works, mining exploitations, and so on.
The study of the convergence behaviour in static PPP shows that we obtain centimetre or millimetre level accuracy after observing for about 3 hours on the latitude, longitude and Ellipsoidal height. The difference between the Static PPP coordinates and the benchmarks is ranged within [20.3cm – 24cm], [17.8cm – 22cm] and [-5.3cm – 6.1cm] respectively over the X, Y and Z-axis. Static PPP can therefore be used in high precision surveyed work.
The assessment of differences between the 03 reading methods and the benchmarks shows that the static PPP positioning with the receiver Emlid Reach RS2 gives better accuracy than kinematic PPP and PPK and can be used to control the stability or to create new benchmarks.
All the tests were performed in the open sky and in an area with small baseline of less than 10km that was in the favour of the low–cost antennas, which are more sensitive to multi-path. To fully evaluate the performance of the low–cost receivers, more tests will be realized in the future over long baselines and real environmental conditions where different factors, such as multi-path, weather conditions, and others, can influence the results.
The difference between the Static PPP coordinates and the Benchmarks is considerable in the case of high precision survey works. Referring to previous studies, this difference is due to either the quality of the antenna used or certain environmental factors.
5. References
Amr H. Ali. (2017). Performance Evaluation of Precise Point Positioning (PPP) Using CSRS-PPP online service. Surveying. American journal of geographic information system, 6(4):156-167.
Ashraf Farah (2013). Effect analysis of GPS observation type and duration on convergence behavior of static PPP. The journal of geomatics, Vol 7 N°2.
Ashraf Farah (2017). GPS staticPPP positioning accuracy variation with observation recording interval for hydrographic applications. Twentieth international water technology IWTC 20 Hurghada, 18-20
Ashraf Farah (2017). Accuracy Assessment Study for Kinematic PPP using Low-Cost GPS Receiver. Al Azhar.14th International conference on engineering, architecture, technology.
Ayhan CEYLAN (2015). Evaluating the Performance of Kinematic PPP and Differential Kinematic Methods in Rural and Urban Areas. FIG working week, sofia Bulgary, 17-21 CSRS-PPP (2021). Canadian Spatial Reference System (CSRS) Precise Point Positioning (PPP) service .http://www. geod.nrcan.gc.ca/productsproduits/ ppp_e.php. Accessed 26/05/2021)
Biagi, L.; Grec, F.; Negretti, M. (2016). Low-Cost GNSS Receivers for Local Monitoring: Experimental Simulation, and Analysis of Displacements. Sensors, 16, 2140.
Broekman, A.; Gräbe, P.J. A. (2021). Low-Cost, Mobile Real-Time Kinematic Geolocation Service for Engineering and Research Applications. HardwareX, 10, e00203. 1.
Gabl, M.; Heller, A. (2021). SmartRTK: Präzise Positionsdaten und Mobile Geodatenerfassung mit Low-CostGNSS—Eine Prototypenentwicklung für Hochalpine Einsätze; Wichmann Verlag: Berlin/Offenbach, Germany.
Garrido-Carretero, M.S.; de LacyPérez de los Cobos, M.C.; Borque Arancón, M.J.; Ruiz-Armenteros, A.M.; Moreno-Guerrero, R.; Gil-Cruz, A.J. (2019). Low-Cost GNSS Receiver in RTK Positioning under the Standard ISO-17123-8: A Feasible Option in Geomatics. Measurement, 137, 168–178.
Guo, L.; Jin, C.; Liu, G. (2017). Evaluation on Measurement Performance of Low-Cost GNSS Receivers. In Proceedings of the 2017 3rd IEEE International Conference on Computer and Communications (ICCC), Chengdu, China, 13–16.
Hamza, V.; Stopar, B.; Ambrosia, T.; Turk, G.; Sterle, O. (2020). Testing Multi-Frequency Low-Cost GNSS Receivers for Geodetic Monitoring Purposes. Sensors, 20, 4375. Hamza, V.; Stopar, B.; Sterle, O. (2021) Testing the Performance of MultiFrequency Low-Cost GNSS Receivers and Antennas. Sensors 21, 2029.
Hamza, V.; Stopar, B.; AmbrožiÄ, T.; Sterle, O. (2018). Performance Evaluation of Low-Cost MultiFrequency GNSS Receivers and Antennas for Displacement Detection. Appl. Sci. 2021, 11, 6666
Ibrahim Murat Ozulu. (2018). Kinematic PPP Positioning using different processing platforms .FIG congress, Istanul, Turkey, may 6-11
Jean-Louis Carme (2012). Le nouveau réseau géodesique du Cameroun, Revue XYZ N°131 2é trimestre
Janos, D.; Kuras, P. (2021). Evaluation of Low-Cost GNSS Receiver under Demanding Conditions in RTK Network Mode. Sensors, 21, 5552.
Krietemeyer, A.; van der Marel, H.; van de Giesen, N.; ten Veldhuis, M.-C. (2020). High Quality Zenith Tropospheric Delay Estimation Using a Low-Cost DualFrequency Receiver and Relative Antenna Calibration. Remote Sens, 12, 1393.
Lapaƒdat, A.M.; Tiberius, C.C.J.M.; Teunissen, P.J.G. (2021). Experimental Evaluation of Smartphone Accelerometer and Low-Cost Dual Frequency GNSS Sensors for Deformation Monitoring. Sensors, 21, 7946.
Leick, A.; Rapoport, L.; Tatarnikov, D. (2015). GPS Satellite Surveying, 4th ed.; Wiley: Hoboken, NJ, USA; ISBN 978-1-118-67557-1
Lipatnikov, L.; Shevchuk, S. (2019). Cost Effective Precise Positioning with GNSS; International Federation of Surveyors: Copenhagen, Denmark; p. 82
Margaria Marie (2020) Évaluation des performances des drones et DGPS à faible coût pour la recherche en géomorphologie côtière. Université via dmitia, Perpignan, France
Muchammad Masykur (2020). Analysis of accuracy the InaCORS BIG online post-processing service. Applied geomatics, https://doi.org /10.1007/s12518-020-00343-2
Omer F. et al. (2021). Investigation of the Kinematic PPP-AR Positioning Performance with Online CSRSPPP Service. FIG e-working Week, 2021, conference paper, 21-25
Nguyen, N.V.; Cho, W.; Hayashi, K. (2021). Performance Evaluation of a Typical Low-Cost Multi-Frequency Multi-GNSS Device for Positioning and Navigation in Agriculture—Part 1: Static Testing. Smart Agric. Technol, 1, 100004.
Odolinski, R.; Teunissen, P.J.G. (2020). Best Integer Equivariant Estimation: Performance Analysis Using Real Data Collected by Low-Cost, Singleand Dual-Frequency, Multi-GNSS Receivers for Short- to Long-Baseline RTK Positioning. J. Geod, 94, 91.
Romero-Andrade, R.; TrejoSoto, M.E.; Vázquez-Ontiveros, J.R.; Hernández-Andrade, D.; Cabanillas-Zavala, J.L. (2021). Sampling Rate Impact on Precise Point Positioning with a Low-Cost GNSS Receiver. Appl. Sci. 11, 7669.
Samboko, H.T.; Schurer, S.; Savenije, H.H.G.; Makurira, H.; Banda, K.; Winsemius, H. (2022). Evaluating Low-Cost Topographic Surveys for Computations of Conveyance. Geosci. Instrum. Method. Data Syst. 11, 1–23
Semler, Q.; Mangin, L.; Moussaoui, A.; Semin, E. (2019). Development of a Low-Cost Centimetric GNSS Solution for Android Applications. In Proceedings of the ISPRS TC II 6th International Workshop LowCost 3D— Sensors, Algorithms, Applications, Strasbourg, France, 2–3 December 2019; Volume XLII-2/W17, pp. 309–314
Teunissen, P.J.G.; Montenbruck, O. (2017). (Eds.) Springer Handbook of Global Navigation Satellite Systems; Springer International Publishing: Cham, Switzerland; ISBN 978-3-319-42926-7.
Tsakiri, M.; Sioulis, A.; Piniotis, G. (2017). Compliance of LowCost, Single-Frequency GNSS Receivers to Standards Consistent with ISO for Control Surveying. Int. J. Metrol. Qual. Eng., 8, 11.
Tunini, L.; Zuliani, D.; Magrin, A. (2022). Applicability of CostEffective GNSS Sensors for Crustal Deformation Studies. Sensors, 22, 350.
Wang, S.; Dong, X.; Liu, G.; Gao, M.; Zhao, W.; Lv, D.; Cao, S. (2022). Low-Cost SingleFrequency DGNSS/DBA Combined Positioning Research and Performance Evaluation. Remote Sens. 14, 586 .
The paper, originally published in Journal of Tertiary and Industrial Sciences Vol 4, No. 1, 2024, is republished with authors’ permission.
The paper to be cited as Benjamin Bahel, Raphael Onguene, Loïc B D Tedongmo, Blaise B Ngwem, Thomas Stieglitz. Multi- band GNSS LowCost Receiver and their Performance in Accuracy. Journal of Tertiary and Industrial Sciences (JTIS), 2024, 4 (1), pp.121-138. hal-04640087.













 (3 votes, average: 2.67 out of 5)
(3 votes, average: 2.67 out of 5)




Leave your response!