Lessons Learned from the Development of GNSS Integrity Augmentations

This paper summarizes some of the important lessons that I have learned over two decades of work on designing integrity augmentations for GPS to support civil aviation.

Sam Pullen Stanford University Stanford, USA

Research and development on methods for supporting “safety-of-life” applications with satellite navigation began well before the achievement of Initial Operational Capability (IOC) of the Global Positioning System (GPS) in 1993. It was known during the development of GPS that the systems that generate GPS ranging signals and navigation data were not designed to meet the very low failure probabilities required for applications like civil aviation. As a result, methods to combine redundant GPS ranging information and/ or to augment GPS with information provided from ground reference systems were developed starting in the mid- 1980’s. Over the past thirty years, Space Based Augmentation Systems (SBAS), Ground Based Augmentations Systems (GBAS), and Receiver Autonomous Integrity Monitoring (RAIM) have been implemented to meet these requirements. Along the way, many worthwhile lessons have been learned.

This paper summarizes some of the important lessons that I have learned over two decades of work on designing integrity augmentations for GPS to support civil aviation. These lessons are intended to illustrate the difficulties inherent in designing integrity into existing systems while retaining sufficient continuity and availability to make the applications that they support economically feasible. These challenges are more than mathematical and require more than simply adding redundancy to mitigate the effects of individual failures.

Lesson 1: GPS and GNSS Satellite Anomalies are Rare

As noted above, the need for augmentation of GNSS comes from the fact that standalone GNSS is not designed to be robust against failures to the probabilities required of civil aviation and other safety-critical applications. Despite this, GPS has proven to have a very low failure rate, and this failure rate has decreased significantly since the initial commissioning of GPS. The fundamental reliability of GPS, as demonstrated over the previous two decades, is key to meeting the demands of these applications.

Failures of individual GNSS satellite measurements can be broken into two classes. The more common type are unscheduled outages or unscheduled failures, meaning the sudden and unexpected loss of measurements due to problems within the GNSS system. These outages put at risk the continuity of user applications because they are unforeseen. In other words, a user that needs measurements from a particular GNSS satellite to complete a given operation (this is known as a critical satellite) and unexpectedly loses that satellite would have to abort his or her operation, causing a loss of continuity. However, since the underlying failure is made evident by the loss of measurements from that satellite (or their being flagged as “unhealthy” by the GPS Operational Control Segment, or OCS), user safety is not threatened beyond any risk that applies to aborting the current operation. The second class of failures, which we can call service failures, do threaten safety because they are not immediately evident to users. In these cases, measurements continue being received without “unhealthy” warnings despite significant ranging errors.

For GPS L1 C/A code, upper bounds for both of these fault types failures are defined in [1]. The probability of unscheduled failures should be no greater than 0.0002 per satellite per hour, given that the satellite was healthy at the beginning of that hour. This probability represents a per-satellite Mean Time Between Outages (MTBO) of 5000 hours, or (at a maximum) slightly more than one unscheduled outage per satellite per year (8766 hours). The probability of service failures, defined in [1] as User Range Error (URE) exceeding 4.42 times the broadcast User Range Accuracy (URA) parameter in the GPS navigation message, is limited to 10-5 per hour per satellite. This probability is equivalent to no more than 3 service failures per year over the entire GPS constellation, assuming a maximum of 32 satellites and a maximum duration of service failures (before they are finally alerted by OCS) of 6 hours. Note that the multiplier of 4.42 corresponds to an exceedance probability of 10-5 for a two-sided standard Gaussian distribution.

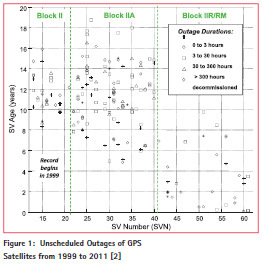
Figure 1 (from [2]) examines the frequency and duration of unscheduled outages of GPS satellites from 1999 to 2011. Each box in this figure represents an unscheduled outage on a particular GPS satellite (indexed by SVN in increasing order on the x-axis), while the age of each satellite at the beginning and end of an outage is shown on the y-axis. The symbol used for each outage indicates the duration of the outage before the satellite was returned to service or (in about 7% of cases) retired. This figure shows that outages are significantly more common with older satellites as their equipment ages and becomes less reliable. Experience with and careful management of older satellites (many of which have lived much longer than their design lifetimes) has reduced the frequency of these outages, particularly in “primary” (as opposed to “spare”) orbit slots. Over this period, the overall probability of unscheduled failures is about 6 × 10-5, or much lower than the bounding probability of 2 × 10-4 given by [1]. Even focusing on SVN 25, which had unusually many outages as it aged, fell just within this probability over the last five years of its lifetime [2].

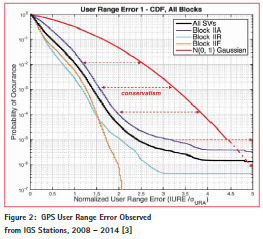
Figure 2 (from [3]) examines the potential for GPS service failures by plotting the distribution (1 minus the cumulative distribution function, or CDF) of URE estimated over time from IGS network station data (collected from 2008 to 2014) normalized by the broadcast onesigma URA. Individual curves are shown for the GPS satellite types active since 2008 as well as the combination of all GPS satellites. All of these curves are exceeded by the standard Gaussian distribution (zero mean, unity variance) shown in red. This figure demonstrates that the broadcast URA bounds the actual URE for GPS satellites that are flagged healthy out to (and beyond) the probability of 10-5 cited in [1] and contains significant margin over the actual error distribution.

The database of GPS observations reported in [3] (and updated in [4]) also allows us to measure the number and duration of actual service failures, meaning specific events where healthy satellites had URE exceeding 4.42 times URA. Since 2008 (after a GPS OCS upgrade in 2007), the number of these events has been far below the three per year across the constellation allowed in [1]. Only five specific service failures have been identified from 2008 to 2015, inclusive (a span of 8 years). These occurred on five different GPS satellites at five different times, meaning that no times existed with multiple GPS service failures. The durations of these events were short, with an average time between onset of the service failure condition and removal from service (e.g., by being flagged as unhealthy or by broadcasting nonstandard code, NSC) of about 21 minutes. Three of these events were diagnosed as satellite clock failures with maximum range errors of approximately 15 – 20 meters. The other two were determined to be errors in the broadcast ephemeris data, one of which (on PRN 19 on 17 June 2012) led to very large errors in the calculated satellite position in space [3].

From these results, the observed service failure onset probability (from 5 events over 8 years and an average of 31 active satellites) is about 2.3 × 10-6 per satellite per hour, which is well below the bounding probability of 10-5 from [1]. In addition, because the average service failure duration is much shorter than the maximum alerting time of 6 hours given in [1], the probability of any given satellite being in a servicefailure state, known as Psat, is about 8 × 10-7, which again is much lower than the numbers that are often assumed.

The very low frequency of GPS satellite faults and their rapid resolution is a product of many years of experience with and improvements to GPS and its Operational Control Segment. Other GNSS constellations, such as Galileo, GLONASS, and Beidou, are either much younger or have had significant architecture changes over their history. The example of GPS suggests that other GNSS constellations can eventually achieve similar reliability, but this should not be taken for granted. Instead, dataanalysis efforts similar to [3] should be conducted so that the performance of newer GNSS constellations can be validated. In the meantime, as with GPS in its earlier years, more conservative probabilities should be used.

Lesson 2: GNSS Anomalies are Difficult to Characterize with Certainty

The fact that GNSS (or at least GPS) satellite anomalies are so rare is a major asset to the design of safety-critical applications of GNSS. However, the very rarity of satellite anomalies makes it difficult to characterize the anomalies that could occur in a manner that allows us to confidently represent their worstcase impacts. In addition to the clock and ephemeris failure modes mentioned above, other satellite faults have either been observed once or twice or have been hypothesized and cannot be excluded. Examples of these include satellite signal deformation and satellite-generated codecarrier divergence. Because observed examples of these events are so few, fault models for these events must be developed by extrapolation (from the few observed events) and engineering judgment [5]. It is thus difficult to have confidence that these models cover all possible faults without being very conservative in constructing them.

Compared to GPS satellite clock failures, which are (or at least were in the past) far and away the most common failure type, large errors in the broadcast ephemeris information have been rare, with few (if any) being observed and confirmed prior to 2007. In the absence of such information, augmentation systems such as SBAS and GBAS needed to hypothesize what kind of failures could occur and what could cause them. Figure 3 (from [6]) summarizes the output of this process for GBAS. It divides potential satellite ephemeris failures into two classes. “Type B” represents an error in generating and broadcasting the ephemeris data for a satellite that has not been maneuvered (i.e., it remains in the same orbit as before), while “Type A” represents an error that is connected with a maneuver of a satellite into a different orbit. Type A, in particular, is divided into subclasses based on the different sequences of events needed to cause them and the way that they would appear to GBAS reference stations.

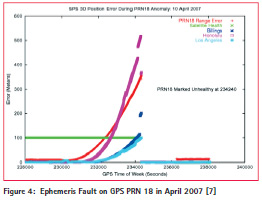
The fault classification and models illustrated in Figure 3 were derived before any examples of significant ephemeris faults were known. However, in April 2007, the Type-A2a event shown in Figure 4 (from [7]) occurred and provided a specific demonstration of what could happen. This fault was caused by a normal (and planned) maneuver of the affected satellite that was not proceeded by setting the satellite “unhealthy.” As a result, when the satellite began its orbit maneuver, users tracking it observed range and position errors that grew and reached several hundred meters before the mistake was realized and the satellite flagged “unhealthy” (and thus unusable). The two ephemeris failures referred to above (from [3]) were observed in 2010 and 2012 and gave us examples of Type B events.

GNSS user safety can also be threatened by unusual behavior in the ionosphere and troposphere through which satellite signals must pass. Both SBAS and GBAS correct for ionospheric errors in different ways, but these corrections can become erroneous under unusually active ionospheric conditions. For GBAS, ionospheric error removal is included as part of the application of pseudorange corrections by users. However, under very anomalous conditions, the spatial difference between ionospheric delays as measured by the GBAS ground system and those measured by users may reach several meters and become hazardous to aircraft precision approaches conducted using GBAS.

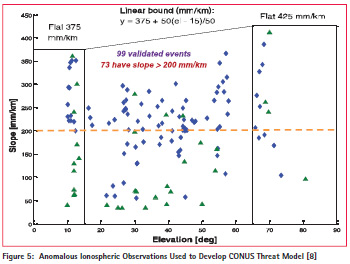
As with the GPS satellite failures discussed earlier, ionospheric anomalies severe enough to create spatial gradients threatening to GBAS users are very rare. As a result, threat models have been developed based on relatively few observed events. Figure 5 (from [8]) summarizes the threat model developed for GBAS use in the Conterminous U.S. (CONUS) based on data collected since 1999. The threat model bounds on spatial gradient as a function of satellite elevation were drawn to include all 99 observations shown on the plot. While 99 observations may seem like a lot, they all occurred on only four days and were all generated by the same physical event (the coronal mass ejection from the Sun that occurred in October of 2003). Furthermore, many of these observations come from multiple nearby reference stations observing the same gradient at about the same time, so they are not really independent. Many more observations than shown here exist for gradients below 200 mm/km, but these are not hazardous to GBAS and therefore do not have any impact on this threat model.

Lesson 3: Safety Requirements for Civil Aviation are Unique, Complex, and Challenging to Meet

Performance requirements for civil aviation applications of GNSS and other navigation systems are specified in terms of accuracy, integrity, continuity, and availability. Of these, meeting integrity for GNSS applications normally implies meeting accuracy as well, but integrity and continuity directly conflict with each other. Integrity is the primary safety requirement, and it mandates that unsafe errors (as defined by each application) not be allowed to persist longer than a specified time to alert except for a specified lossof- integrity probability (or “integrity risk”). Continuity affects both safety and operational efficiency and mandates that the probability of aborting an operation after it has begun is lower than a specified loss-of-continuity probability. The primary means of protecting integrity once an unsafe error is detected is to remove the affected measurements, but doing so increases the risk of loss of continuity.

If an unsafe error is present, this is still appropriate (integrity takes precedence), but in practice, many integrity monitor alerts come from fault-free noise, better known as “false alarms.” In short, adding monitoring to meet the integrity requirement comes at a cost in continuity.

Availability can be expressed as the probability that all other requirements are met at a given time and requires that both integrity and continuity be met simultaneously. This is a challenge for any safety-critical application but is especially so for civil aviation because of the way in which the integrity requirement is interpreted. The loss-of-integrity probability for civil aviation must be computed using a concept known as “specific risk,” which is non-standard and can be complicated to interpret. It is easier to explain specific risk in contrast to the alternative of “average risk,” which is more commonly encountered. Under average risk, if a failure event may take on many different sets of characteristics, only some of which may lead to loss of integrity (the “hazardous subset”), credit may be taken for the probability of falling outside the hazardous subset. This is important in practice, as the “hazardous subset” for many failure types is small. However, under specific risk, credit cannot be taken for this – the “worst-case” outcome of a particular fault mode, from the point of view of the system being evaluated, must be assumed to occur with a probability of 1 (given that the fault occurs) [9].

The need to quantify and bound the worstcase effects of each type of fault is what drives the need to create conservative fault models for civil aviation. As explained above, most GNSS fault models are based on few actual fault observations; thus it is difficult to conclude that the worst-case fault is simply the worst of the events that have been observed in the past. The worst-case fault is often derived from expert consensus as an extrapolation from the observed events plus a simplified physical model of how these events occur. The extrapolated model can be used to simulate the impact of the underlying fault on a particular GNSS application and to determine which combination of fault parameters gives the worst results for that application (it is not always obvious).

Lesson 4: Significant Design Conservatism is Needed to Verify that Civil Aviation Requirements are Met

The result of applying Lessons 1, 2, and 3 is that significant conservatism is needed in both the design of GNSS augmentations for civil aviation and the verification that these augmentations provide the required integrity and continuity. Lesson 1 shows that GPS failures to date, particularly those that might threaten integrity, are very rare. Unfortunately, they are not so rare that their probability can be neglected. As explained in Lesson 2, the consequence is that few examples of actual failure events exist to be used in modeling the range of possible failures. Absent a statistically significant number of events, a wide range of possibilities must be considered, and it is difficult to draw a line between what is possible (albeit rare) and what is “non-credible.” Lesson 3 explains that, at least for civil aviation, the evaluation of integrity risk under each “credible” fault condition must be based on the worst-case combination of parameters that describe that fault.

Figure 6 (from [10]) illustrates the resulting conservatism from results of the U.S. Wide Area Augmentation System (WAAS), an example of SBAS, in the 3rd quarter of 2010. This is a “triangle plot” in which the actual WAAS vertical position errors (VPE) observed over a network of ground stations with known locations are compared to the vertical protection levels (VPL) computed at the same locations and times. Protection levels are an important concept in GNSS integrity – they express the maximum position error that could occur at the probability for which the protection level is derived, which is based on the specified integrity risk for that application (in this case, it is 10-7 per 150 seconds, corresponding to a typical LPV-200 aircraft precision approach).

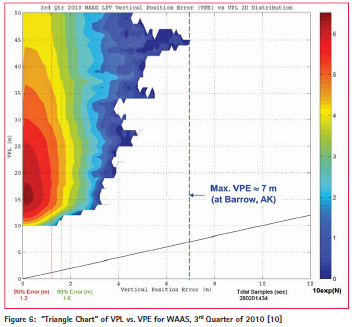
What is notable is the ratio between the actual VPEs and the calculated VPLs, which are based on the user’s satellite geometry and integrity parameters (bounding error sigma values) broadcast by WAAS. During this typical 3-month period for WAAS, the 95th and 99thpercentile vertical errors were 1.2 and 1.6 meters, respectively, while the maximum vertical error was about 7 meters in Barrow , Alaska, near the very edge of WAAS coverage. In contrast, typical VPLs were in the range of 15 to 30 meters and occasionally exceeded 35 meters, the limit for LPV-200 precision approaches. The reason for this gap is that VPL is not meant to reflect typical or even unusual conditions. Rather, it expresses the potential impact of the worst combination of parameters among all of the anomalous threat models that apply. For WAAS, this is driven by the worst possible ionospheric spatial decorrelation that might go unobserved. While this event is exceedingly improbable, it cannot be excluded from the “specific risk” calculation of civil aviation integrity.

Summary

This paper describes lessons learned from my experience in the development of safety-critical GNSS applications for civil aviation. They show how the challenges to integrity and continuity design and verification differ from maximizing performance in typical GNSS environments. While GPS satellite failures that threaten integrity have historically been rare, the limited number of observed failures makes it difficult to build models that can be assured to bound worst-case failure events with certainty. The strict interpretation of integrity risk applied by civil aviation places great weight on these bounds, thus a great deal of conservatism must be introduced in the development of threat models and the application of them to the calculation of protection levels by users in real time.

The implementation of GNSS integrity to support civil aviation is highly relevant to other safety-critical applications on land, sea, and air, even if they do not share the same “specific risk” approach to safety assessment. Under the “average risk” interpretation, the development of threat models would focus less on the worst possible events and more on an appropriate probabilistic description of the range of possible events resulting from a given failure mode [5, 9]. The result would be significantly less conservatism and a smaller gap between nominal performance and integrity guarantees.

References

[1] Global Positioning System Standard Positioning Service Signal Standard (GPS SPS PS), 4th Ed, Sept. 2008 (U.S. Dept. of Defense, Washington, DC, 2008). http:// www.gps.gov/technical/ps/2008- SPS-performance-standard.pdf

[2] S. Pullen and P. Enge, “Using Outage History to Exclude High-Risk Satellites from GBAS Corrections,” Navigation, Vol. 60, No. 1, Spring 2013, pp. 41-51. http://waas. stanford.edu/papers/Pullen_Outage HistoryExcludeHighRiskSatellites_ v60n1.pdf

[3] T. Walter and J. Blanch, “Characterization of GPS Clock and Ephemeris Errors to Support ARAIM,” Proceedings of ION Pacific PNT 2015, Honolulu, HI, April 20-23, 2015, pp. 920-931. http://waas.stanford. edu/papers/Walter_IONPNT_2015_ ARAIM_characterization.pdf

[4] T. Walter, “History of GPS Performance,” Stanford GPS Laboratory Meeting, June 17, 2016 (unpublished).

[5] S. Pullen, “The Use of Threat Models in Aviation Safety Assurance: Advantages and Pitfalls,” Proceedings of CERGAL 2014, Dresden, Germany, July 7-9, 2014.

[6] H. Tang, S. Pullen, et al, “Ephemeris Type A Fault Analysis and Mitigation for LAAS,” Proceedings of IEEE/ ION PLANS 2010, Indian Wells, CA, May 4-6, 2010, pp. 654-666. http://waas.stanford.edu/papers/ Tang_IEEEIONPLANS_2010_ EphemerisTypeAFault MitigationforLAAS.pdf

[7] “Global Positioning System (GPS) Standard Positioning Service (SPS) Performance Analysis Report,” William J. Hughes Technical Center, Atlantic City, NJ, Report #58, July 31, 2007. http://www.nstb.tc.faa. gov/REPORTS/PAN58_0707.pdf

[8] M. Kim, J. Lee, S. Pullen, and J. Gillespie, “Data Quality Improvements and Applications of Long-Term Monitoring of Ionospheric Anomalies for GBAS,” Proceedings of ION GNSS 2012, Nashville, TN, Sept. 17-21, 2012, pp. 2159- 2174. http://ion.org/publications/ abstract.cfm?articleID=10410

[9] S. Pullen, T. Walter, and P. Enge, “SBAS and GBAS Integrity for Non-Aviation Users: Moving Away from ‘Specific Risk’”, Proceedings of ION ITM 2011, San Diego, CA, Jan. 24-26, 2011, pp. 533-545. http://waas.stanford.edu/papers/ Pullen_IONITM_2011_Integrity_ for_Non-Aviation_Users.pdf

[10]“Wide-Area Augmentation System Performance Analysis Report,” William J. Hughes Technical Center, Atlantic City, NJ, Report #34, October 2010. http://www.nstb.tc.faa.gov/ REPORTS/waaspan34.pdf