| Geodesy | |
Classroom Geodesy
|
||||
|
Geodesy is science of the measurement and mapping of the earth’s surface. Satellite Geodesy in an orderly intensive manner started with the launch of the first artificial satellite SPUTNIK in October 1957. By the year 1964, many basic geodetic problems had been successfully tackled. Most significant of the problems tackled are determination of a precise numerical value of the earth flattening, determination of the general shape of the global geoid and determination of connections between the most important geodetic datums. Since 1980 satellite methods are increasingly used by the surveying community replacing the conventional methods. This process started with the first results obtained with he NAVSTAR Global positioning System (GPS). The applications of geodetic satellite methods are determined by the achievable accuracies. Some of the applications are cited as follows: • Establishment of global terrestrial reference frame • Establishment of Geodetic control for national networks • Control points for crustal motions • Terrestrial control points in photogrammtery and remote sensing • Control points for cartography during expeditions • Detailed surveying for land records, LIS, GIS, town planning and boundary demarcation etc • Position and velocity determinations for geophysical observations • Precise positioning for marine mapping, marine geology, bathymetry and connection of tide gauges The list is by no means could become exhaustive but only illustrative as there is no limit technically for the possible applications. The physical shape of the real earth is closely approximated by the mathematical surface of the rotational ellipsoid. The ellipsoid surface is smooth and convenient for mathematical operations. This is why the ellipsoid is widely used as the reference surface for horizontal coordinates of geodetic networks. For most practical applications ellipsoidal coordinates systems are preferred because they closely approximate the earth’s surface and they facilitate a separation of horizontal position and height. Usually a rotational ellipsoid is selected which is flattened (f) at the poles and which is created by rotating the meridian ellipse about its minor axis b. Here ais major axis. The geometric parameter On the other hand the ellipsoid is much less suitable as a reference for vertical coordinates (heights). Instead the geoid is used It is defined as that level surface of the gravity field which best fits the mean sea level, and may extend inside the solid body of the earth. The vertical difference between geoid and a particular reference ellipsoid is called geoid undulation. Appropriate well defined and reproducible reference coordinate systems are essential for the description of satellite motion. Reference coordinate systems is satellite geodesy are global and geocentric because the satellite motion refers to the centre of the earth. Terrestrial coordinate systems are generally local and represented by local coordinate systems The relationships between the both the systems must be known with sufficient accuracies. As such we will deal with reference coordinate system in satellite Geodesy in the next issue.. The Coordinates Class room espouse readers to graticules of Mathematics and Physics that epitomize the Geospatial Information Technology. A chain of structured presentations related to interdisciplinary principles that define Geodesy, GPS, GIS, Geospatial data management and Image processing are to be en suite in this section in each issue of the Coordinates. Initially the chain trembles with Geodesy which is the mother of technologies to position the Coordinates. |
||||


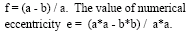










 (No Ratings Yet)
(No Ratings Yet)





