| Positioning -New | |
A stand-alone positioning method for kinematic applications
In this study, an algorithm is proposed to improve the positional accuracy within a few decimeters using a single geodetic receiver with carrier phase data |
 |
|
 |
|
 |
|
GNSS-based positions can be obtained in two general ways – Absolute (or Autonomous) Positioning and Differential (or Relative) Positioning. Absolute positioning, with only a single receiver, allows a meter level positioning easily and continuously. It has been widely used for several civil and military applications in real-time with only use of a single GNSS receiver. Although the absolute positioning accuracy has been significantly enhanced via the GNSS modernization studies, this accuracy is not regarded as sufficient for many surveying applications.
Over the past decade, a number of techniques have been introduced in literature to improve the positioning accuracy by using a single GNSS receiver. For example, in the 1980s, some researchers employed a method called ‘smoothing’ to create a pseudorange/ carrier phase combination that smoothes the pseudo-range data and could do point positioning at a meter or sub-meter level of accuracy, but it still did not meet the requirements of many surveying applications (Saka et al., 2004).
Latest developments in GNSS data analysis and processing techniques offer some new approaches. A new method, called Precise Point Positioning (PPP), has arisen from the advent of widely available precise satellite orbits and clock data products provided from many organizations, such as International GNSS Service (IGS), Jet Propulsion Laboratory (JPL), NRCan and others. The PPP method provides positioning within a centimeter to decimeter level of accuracy using a single GNSS receiver data in static and kinematic modes (Zumberge et al., 1997; Kouba and Héroux, 2001; Choy et al., 2007; Huber et al., 2010; Alkan and Öcalan, 2013). Furthermore, for accurate PPP solutions, a number of corrections (e.g., carrier-phase wind-up, satellite antenna phase center, solid earth tide and ocean loading) should also be taken into account.
Although the PPP technique has been widely used and has become more popular, it has some drawbacks such as the necessity of long occupation time for convergence and the unavailability of PPP processing mode in common commercial GNSS processing software. The long convergence time restricts its usability in many cases where rapid solution is required and surveying efficiency is concerned (Liu et al., 2013).
In our study, an algorithm is developed for precise positioning in dynamic environment utilizing dual-frequency GNSS carrier phase data collected only with a single geodetic-grade receiver. In this method, users should initiate the measurement on a known point near the project area for only a couple of seconds before starting the kinematic measurements. The technique employs iono-free carrier phase observations with precise orbit and clock products. The equation of the algorithm is given below;
![]()
where, Sm(ti+1) is the phase-range between satellites and the receiver, SC(ti) is the initial range computed from the initial known point coordinates and the satellite coordinates and ΦIF is the ionosphere-free phase measurement (in meters) (Saka and Alkan, 2014). Tropospheric path delays are modelled using the Simplified Hopfield Model.
To accomplish the process, an in-house program was coded in MATLAB and some functions were adopted from Easy-Suite available at http://kom.aau. dk/~borre/easy (Borre, 2003). More detailed information about the handled algorithm can be found in Saka and Alkan (2013 and 2014); Saka et al., (2015).
In this study, the usability of the introduced algorithm in near-shore kinematic applications is investigated. For this purpose, a test measurement was carried out in Istanbul, Turkey and the performance of the algorithm was assessed. In this paper, the test procedures and their results are briefl y discussed.

Case study
In order to assess the performance of the introduced algorithm in a dynamic environment, a dataset from a kinematic test measurement was used. The data were collected from a kinematic test measurement in Haliç Bay (commonly known as the Golden Horn), Istanbul, Turkey in August 2009 (Figure 1).
In the test measurement, a geodetic-grade dual-frequency GPS receiver, Ashtech Z-Xtreme, was set up on a known point on the shore and a couple of epochs were recorded for initialization. The receiver was then moved to a vessel and data were collected for approximately 2.5 hours (Figure 2). The measurement was finalized on a known point on the shore.
While the kinematic measurements on the vessel were carried out, another GNSS receiver was set up on another geodetic point with known coordinates in ITRF reference frame on the shore and data were collected in static mode. The collected data by geodetic receivers, both on vessel and occupied on the shore, were processed by the Leica Geosystems commercial GPS processing software, Leica Geo Office (LGO). In this way, it is possible to obtain the reference trajectory with differential technique, i.e., known-coordinates of the vessel for each epoch that allows to perform precise assessment of the introduced approach.
The coordinates of the vessel were calculated for each measurement epoch with the introduced method. As seen from Eq. 1, the process starts with the computing of distance between the observed satellites and the known point that measurements are initiated. After the first measurement, the change in the range between previous epoch and current epoch measured by the carrier phase is added to the previous range to determine the next phase-range. Then positions of the vessel are estimated for every epoch using phase-ranges (Saka and Alkan, 2014). In this study, with the purpose of obtaining more robust results, all coordinates were calculated once again inversely. As stated earlier, the test measurements ended up at a control point where coordinates were known precisely in ITRF datum. The process was run from last epoch to the first one and coordinates of the vessel were determined once again. The main purpose of this approach is to minimize the time-dependent error propagation. Furthermore, the calculated coordinates were also controlled. The average of estimated coordinates from two approaches was used as vessel coordinates. Positions of the vessel estimated from the introduced algorithm were compared with the known-coordinates epoch by epoch. The differences in north, east, positions and ellipsoidal heights are shown in Figure 3.
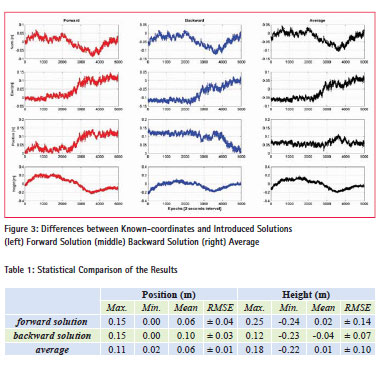
The statistical comparison of the results as minimum, maximum, mean differences and root mean square of the error (RMSE) are summarized in Table 1.
It is clearly shown in Figure 3 and Table 1 that the coordinates from the introduced method agree with the relative solution reaching to 11 cm and 22 cm for position and height respectively by the averaging of both estimated coordinates (i.e., calculated from first epoch to last epoch and from last epoch to first epoch). The differences were found relatively poor for the height components within about 2 dm or better accuracy. In general, the averaged-coordinates from the introduced method agree with the differential method within 1-dm or better level of accuracy for position and 2-dm or better level of accuracy for height.
Conclusions
In this study, an algorithm is proposed to improve the positional accuracy within a few decimeters using a single geodetic receiver with carrier phase data. The results produced in this study showed that decimeter level positional accuracy could be achieved with the introduced algorithm. This level of accuracy can be acceptable for a variety of surveying and mapping applications, including some marine applications, precise hydrographic surveying, dredging, attitude control of ships, buoys and fl oating platforms, marine geodesy, navigation and oceanography.
Acknowledgement
This paper is an extended and reviewed version of the study that was presented at the European Geosciences Union General Assembly 2015, Vienna, Austria, 12–17 April 2015.
References
Alkan, R.M. and Öcalan T. (2013). Usability of GPS Precise Point Positioning Technique in Marine Applications, Journal of Navigation, 66(4), pp. 579-588.
Borre, K. (2003). The GPS Easy Suite- Matlab Code for the GPS Newcomer,GPS Solutions, 7(1), pp. 47–51.
Choy, S.L., Zhang, K., Silcock, D. and Wu, F. (2007). Precise Point Positioning-A Case Study in Australia,In Proc. of Spatial Sciences Institute International Conference (SSC2007), pp. 192- 202, Hobart, Tasmania, Australia.
Huber, K., Heuberger, F., Abart, C., Karabatic, A., Weber, R. and Berglez, P. (2010). PPP: Precise Point Positioning- Constraints and Opportunities, XXIV FIG International Congress, Sydney, Australia, April 11-16.
Kouba, J. and Héroux, P. (2001). Precise Point Positioning Using IGS Orbit and Clock Products, GPS Solutions, 5(2), pp. 12-28.
Liu, Z., Ji, S., Chen, W. and Ding, X. (2013). New Fast Precise Kinematic Surveying Method Using a Single Dual- Frequency GPS Receiver,Journal of Surveying Engineering, 139(1), pp. 19-33.
Saka, M.H., Kavzoglu, T., Ozsamli, C. and Alkan, R.M. (2004).Sub-Metre Accuracy for Stand Alone GPS Positioning in Hydrographic Surveying, Journal of Navigation, 57(1), pp. 135–144.
Saka, M.H. and Alkan, R.M. (2013). An Approach for Decimeter-Level Positioning by Using Single Receiver in Hydrographic Applications, Abstract Book of The 2nd International Conference on: Measurement Technologies in Surveying-GTP 2013, pp. 35-36, Warsaw, Poland, 23–25 May.
Saka, M.H. and Alkan, R.M. (2014). Decimeter-level Positioning in Dynamic Applications with a Single GPS Receiver, ActaGeodaetica et Geophysica, 49(4), pp. 517-525.
Saka, M. H., Alkan, R.M. and Özperçin, A. (2015). An Approach for Highprecision Stand-alone Positioning in a Dynamic, EGU General Assembly 2015, Geophysical Research Abstracts, Vol. 17, EGU2015-7378.
Zumberge, J.F., Hefl in, M.B., Jefferson, D.C., Watkins, M.M. and Webb, F.H. (1997). Precise Point Positioning for the Efficient and Robust Analysis of GPS Data from Large Networks, Journal of Geophysical Research, 102(B3), pp. 5005-5017.












 (39 votes, average: 4.77 out of 5)
(39 votes, average: 4.77 out of 5)




Leave your response!